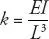John Long - Darwin’s Devices

Genetic drift, in the absence of selection, produces evolutionary change in directions that are random with respect to both phenotype and genotype. Because drift is random, neither it nor any other random mechanism will produce the kind of long-term directional pattern that we recognize as the signal of adaptation. Only selection is equal to the task.

For our tiny population of Tadro3s, the absence of selection in some generations allows the combined random chance of two sources of randomness—mutation and genetic drift—to be the prime movers. Over a generation or two, we can even be fooled. Our population can be “on a roll” that may look like a directional and evolutionary trend. This is what happened to the average feeding behavior from generations 2 through 4. Random changes just happen to have combined to decrease the feeding behavior. Chance favors no one.

What’s really important to keep in mind, and to keep Darwin from being on a roll in his grave, is that over generational time random changes—which occur with or without selection—are, indeed, mechanisms of evolutionary change. This fact is worth restating: you can have evolution with or without selection. We’ve shown this to be true with our population of Tadro3s. It’s also worth pointing out that the random genetic processes are always occurring and that they operate independently from selection. There is a third mechanism influencing how populations evolve, however: history (Figure 4.2). [36] Students and scholars of evolutionary theory will be quick to interject, what about sexual selection, gene flow, genetic drift, epistasis, mating, and developmental processes as evolutionary mechanisms? True. Those are other identifiable mechanisms of evolutionary change. Lenski’s point, which I follow here, is that any mechanism fits into a category of either being deterministic or random. Natural selection is deterministic in that once you identify all of Brandon’s information (see Chapter 2), you can predict evolutionary outcome. Random factors like mutation or assortative mating have outcomes that are not predictable. I continue to be influenced by this fascinating and illuminating paper: M. Travisano, J. A. Mongold, F. Bennett, and R. E. Lenski, “Experimental Tests of the Roles of Adaptation, Chance, and History in Evolution,” Science 267, no. 5194 (1995): 87–90. Also, you may be interested in the Neutral Theory of molecular evolution, which is based on the idea that most random genetic changes have no effect on selection. In the face of genomic data, this idea is rapidly changing: Matthew W. Hahn, “Toward a Selection Theory of Molecular Evolution,” Evolution 62, no. 2 (2007): 255–265. The independence of these three kinds of mechanisms was beautifully demonstrated by Professor Rich Lenski, of Michigan State University, in his work first on bacteria and then on what he calls “digital organisms.” Lenski showed that the genetic and phenotypic variation that exist in your population at any time constrain the population’s future evolutionary possibilities. Any finite population can only evolve in certain directions, directions that are constrained by the underlying genetic coding of the phenotypes and the responses of individual organisms to the particular environment. Another way to think of this history effect is that selection can only select, as we saw in the Tadro3 generations 2 through 4, when individuals vary. Selection can only result in evolution-by-selection when genes code, at least in part, those individual variations.

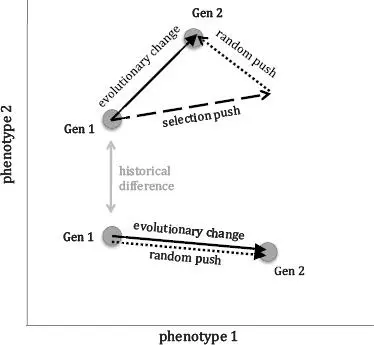
FIGURE 4.2. Selection, random processes, and history interact to create evolutionary change in a population. The dots represent the average position of the population in “morphospace,” the realm of evolutionary possibility represented by the ranges of phenotype 1 and phenotype 2. History determines where in the morphospace a population starts as well as the nature of the genetics underwriting the phenotypes. Evolutionary change is the movement of the population, over generational time, in response to either (1) selection and random processes (top population) or (2) random processes alone (bottom population). Selection is unlikely to act without random genetic processes because the continual creation of genetic variation is needed to make the phenotypic variations from which the fitness function selects.

For our population of Tadro3s, history covers a multitude of sins or, more accurately, assumptions. Our Tadro3s didn’t first evolve from single-celled Tadro0.001s, so they don’t have an explicit evolutionary history, but they do have an implicit one: the evolutionary history of the tunicate tadpoles after which Tadro3s are modeled. That tunicate history has bequeathed Tadro3s a notochord, a light-sensitive organ, a brain capable of linking sensor and undulating tail, and the genes that underwrite these phenotypes. History has also brought along environmental baggage—the water with a directional light source in which Tadro3 lives.

History’s most important legacy for Tadro3s is the blood line, the initial genetic conditions—essentially the genes and the variants of those genes that we decided Tadros had. Because we were interested in structural stiffness of the notochord and, by extension, the tail in which the notochord sits, we coded for that property and placed its initial value in the middle of a scale of biological stiffnesses.

Structural stiffness is a property that describes how a structure will change shape when an external force acts on it. Think about a cantilevered structure, like a flagpole hung horizontally. When you put a flag on the pole, it bends down slightly. Or, better yet, imagine that old Three Stooges movie short, Flagpole Jitters , in which Moe, Larry, and Shemp find themselves hypnotized and walking out on a flagpole high above the city streets. Through experiments with weights rather than clinging Stooges, engineers have figured out that the structural stiffness of a cantilevered beam like a horizontal flagpole is proportional to the beam’s flexural stiffness and inversely proportional to the cube of the beam’s length. This is one of those moments when, against the advice of my friends, I just can’t help but use an equation to summarize all of this:

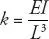
To clarify, what this equation says is that structural stiffness, represented by the variable k (in units of Newtons per meter) is defined as the ratio of the flexural stiffness, the composite variable EI (in units of Newton square-meters), to the cube of length, L 3(units of cubic meters). What’s nifty about this equation is that you can see right away what matters. Want a stiffer beam? Increase the EI or decrease the L . A longer cantilever has a huge impact on k because of the cubing of the L . An equation like this also helps conjure up the genetics we’re after.

We could have just said that Tadros have genes that code for k directly and then left it at that. However, research on biological stiffness suggests that all three variables, E , I , and L can change independently during development and evolution. The variable E (in measurement units of Newtons per square meter) by itself is called by a variety of names: “modulus,” “elastic modulus,” “complex modulus,” “Young’s modulus,” or “Young’s modulus of elasticity.” Too many aliases! But wait—let me do my part for the witness protection of E . Because E is part of structural stiffness, k , and flexural stiffness, EI , and is caused by the kind and number of chemical bonds in the material you’re dealing with, I prefer to call it “material stiffness.” [37] For completeness, I should tell you that the variable I (in units of meters to the fourth power) is called the “second moment of area.” The second moment of area is a geometric property of how the structure’s material is arranged and clustered in cross-section, the plane perpendicular, to, in this case, the long axis of our beam that we measure with the variable L .