Многочисленные измерения фенотипических дистанций позволяют прийти к некоторым выводам, довольно существенным для нашей темы. Во-первых, для многих совсем не родственных видов животных средние расстояния между популяциями одного вида обычно весьма близки, и, во-вторых, для морфологических дистанций, отделяющих виды одного рода, также характерен свой средний уровень, который, как правило, в 1,5–2 раза превосходит межпопуляционный. Эти результаты наводят на мысль, что превращение популяций в виды сопряжено с достижением их особями вполне определенного значения относительного сдвига величины ряда количественных признаков. Что же происходит с видом в момент видообразования? Очевидно, приспособление к новым экологическим условиям.
Хорошо известно, что для каждого вида ряд жизненно важных параметров среды не должен выходить за пределы некоторых критических значений. Так, для жизни рифообразующих коралловых полипов необходимо, чтобы температура воды не опускалась ниже 20,5 °C. Полный комплекс требований вида к параметрам среды может быть объединен понятием экологической ниши вида. Таким образом, каждому виду соответствует его экологическая ниша. В одной нише устойчиво может существовать только один вид (принцип Гаузе), если вдруг по какой-то причине в ней окажутся два, то со временем один из них уступит место другому, скорее всего, он вымрет. Филетическое выживание вида (видообразование) сопряжено с его переходом в соседнюю экологическую нишу, при этом же, очевидно, происходят сдвиги значений многих количественных признаков особей. Мы уже отмечали (см. параграф «Аллометрия» в гл.2), что сдвиги подобного рода обычно связаны с изменением абсолютных размеров структур и прежде всего с изменением средней массы животного.
Знаменитый американский эколог Дж. Хатчинсон предположил, что для завершения экологической дифференциации средняя величина морфологического признака, непосредственно ответственного за адаптацию, должна измениться в какое-то фиксированное число раз. Оказалось, что довольно часто выполняется одно удивительное правило: массы особей родственных видов животных, обитающих в одной местности (т. е. в сходных экологических условиях), отличаются друг от друга в число раз, примерно кратное двум. Как будто для экологического разобщения особи таких видов должны различаться по массе примерно в 2 раза. Из этого правила Хатчинсона следует, что линейные размеры тела отличаются минимум в 2 1/3≈ 1,26 раза, или, грубо, на 30 %. Особенно четко это правило выполняется для размеров пищедобывающих структур животных. Прямые измерения показывают, что чаще всего линейные размеры этих структур ( L ) отличаются, как минимум, на 28 %. Отсюда вытекает, что размер L можно представить как некую минимальную величину L min, умноженную на произведение ряда сомножителей х i, близких к 1,28, т. е.
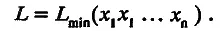 (5.1)
(5.1)
После логарифмирования этого выражения имеем
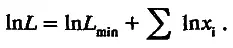 (5.2)
(5.2)
Заметим, что ∑ln x iпредставляет собой сумму близких по порядку независимо варьирующих величин, поэтому распределения большого числа видов по логарифму размеров или массы особей должны быть близкими к нормальным.
Формирование видовых распределений
Построим простейшую модель видовых распределений. Будем считать, что для экологической дифференциации видов их особи должны отличаться по размерам на 28 %, соответственно натуральный логарифм их размеров — приблизительно на 0,25. Разобьем горизонтальную ось, вдоль которой изменяется логарифм линейных размеров, на интервалы шириной 0,25. Пусть вид-основатель филетической группы по размеру своих особей находился в интервале х 0. Через единичный отрезок времени (через один шаг модели) он произведет два дочерних вида, которые попадут в соседние интервалы х -1, и х 1. Отметим, что интервал х 0 остается занятым материнским видом. В следующий временной отрезок каждый из трех видов приступит к «завоеванию» своих соседних интервалов. Продолжая такой процесс, мы вскоре получим довольно гладкое симметричное (биномиальное) распределение, очень близкое к нормальному. С каждым шагом оно расширяется, его дисперсия увеличивается пропорционально возрасту таксона, а сигма следует за квадратным корнем из этого возраста. Однако центр тяжести распределения (его среднее значение) должен оставаться на месте, точно соответствуя величине признака у вида-основателя филетической группы — х 0(рис. 18, а).
Читать дальше

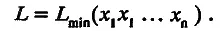 (5.1)
(5.1)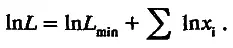 (5.2)
(5.2)







