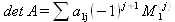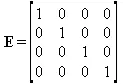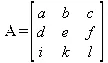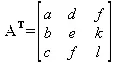Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Возможно представление интеграла и в полярной системе координат. Пример этого дан на рис. 5.38.

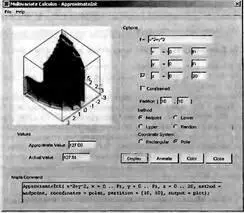
Рис. 5.38. Maplet-окно демонстрации приближенного вычисления двойного интеграла в полярной системе координат

Команда Cross Section… открывает Maplet-окно демонстрации сечения поверхности плоскостями. Поверхность задается функцией двух переменных z(x, у). Окно этой команды представлено на рис. 5.39.

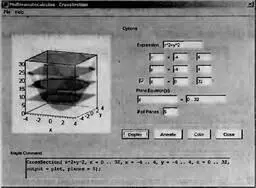
Рис. 5.39. Maplet-окно демонстрации сечения поверхности параллельными плоскостями

Работа с этим окном вполне очевидно. На рисунке в левой части окна строится исходная поверхность, секущие плоскости и линии их пересечения.

Задачи линейной алгебры, оптимизации и регрессии — одни из самых массовых в науке, технике и образовании [37, 39–46]. Им и посвящена эта глава. В ней даны основные определения линейной алгебры, основы работы с массивами, векторами и матрицами, функции для работы с векторами и матрицами и для решения систем линейных уравнений. Дано описание средств оптимизации, в том числе новейших системы Maple 10.

Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple в решении задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.

Матрица (m×n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3×3:

Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

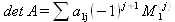
где M 1 — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j- го столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Сингулярная (вырожденная ) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4×4:

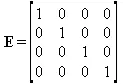
Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы transpose(A)∙А, где transpose(A) — транспонированная матрица А (см. ее определение ниже).

Транспонированная матрица — матрица, у которой столбцы и строки меняются местами, то есть элементы транспонированной матрицы удовлетворяют условию A T(i,j)=A(j,i). Приведем простой пример.

Исходная матрица:

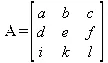
Транспонированная матрица:

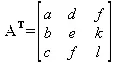
Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.