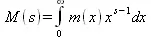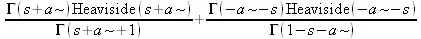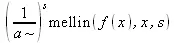Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Интегральное преобразование Меллина задается выражением

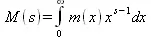
и реализуется функцией

mellin(expr, x, s)

с очевидными параметрами expr, x и s. Применение преобразования Меллина иллюстрируют следующие примеры:

> assume(а>0);

> mellin(x^a,x,s);

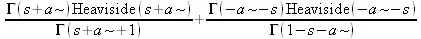
> mellin(f(а*х),х,s); mellin(f(a*x), x, s);

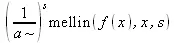
> invmellin((gamma+Psi(1+s))/s,s,x,-1..infinity);

Примеры на применение преобразования Меллина можно найти в файле mellin.mws.

Как видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция

addtable(tname,patt,expr,t,s)

где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны. Следующие примеры поясняют применение этой функции:

> fouriersin(f(t),t,s);

> addtable(fouriersin,f(t),F(s), t,s);

> fouriersin(f(x),x,2);

В этой главе до сих пор рассматривались точные функции преобразования или представления аналитических функций. Однако часто возникает и другая задача — некоторую совокупность данных, например заданных таблично, надо приближенно представить некоторой известной аналитической функцией. Эта задача решается регрессионным анализом или просто регрессией. Параметры приближающей функции выбираются так, что она приближенно (по критерию минимума среднеквадратической ошибки ) аппроксимирует исходную зависимость. Последняя, чаще всего, бывает представлена некоторым набором точек (например, полученных в результате эксперимента).

Наглядная визуализация регрессии была рассмотрена выше — см. рис. 5.23. А теперь рассмотрим типовые средства проведения регрессии (файл regres).

Для проведения регрессионного анализа служит функция fit из пакета stats, которая вызывается следующим образом:

stats[fit,leastsquare[vars,eqn,parms]](data)

или

fit[leastsquare[vars,eqn,parms]](data)

где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.

На приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х):

> with(stats):Digits:=5;

> fit[leastsquare[[x,у]]] ([[1, 2, 3, 4], [3, 3.5, 3.9, 4.6]] );

> fit[leastsquare[[x,y, y=a*x^2+b*x+c]] ([[1,2,3,4], [1.8,4.5,10,16.5]]);

В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, а функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией в виде полинома, осуществляя полиномиальную регрессию.

Рисунок 5.29 показывает регрессию для одних и тех же данных полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных.

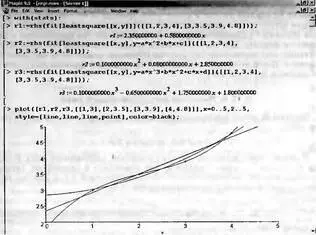
Рис. 5.29. Примеры регрессии полиномами первой, второй и третьей степени

Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов.