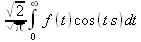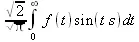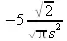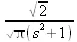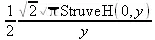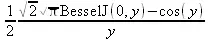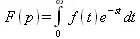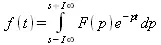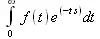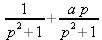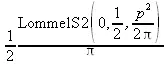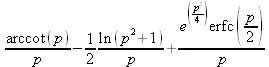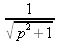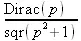Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Для вычисления этих интегралов в пакете используются следующие функции:

fouriercos(expr,t,s)

fouriersin(expr,t,s)

Поскольку формат задания этих функций вполне очевиден, ограничимся примерами визуализации сути этих функций и примерами их применения:

> convert(fouriercos(f(t),t,s),int);

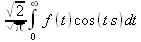
> convert(fouriersin(f(t),t,s),int);

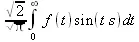
> fouriercos(5*t,t,s);

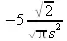
> fouriersin(5*t,t,s);

> fouriercos(exp(-t),t,s);

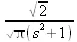
> fouriercos(arccos(х) * Heaviside(1-х), х, y);

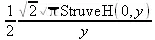
> fouriersin(arcsin(x) * Heaviside(1-х), x, y);

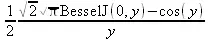
Нетрудно заметить, что эти преобразования нередко порождают специальные математические функции. Много примеров на преобразования Фурье содержатся в файле демонстрационных примеров fourier.mws.

Преобразования Лапласа — одни из самых часто применяемых интегральных преобразований. Они широко применяются в электрорадиотехнике и часто используются для решения линейных дифференциальных уравнений.

Прямое преобразование Лапласа заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла

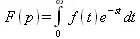
Для осуществления прямого преобразования Лапласа служит функция

laplace(expr,t,р)

Здесь expr — преобразуемое выражение, t — переменная, относительно которой записано expr, и p — переменная, относительно которой записывается результат преобразования.

Обратное преобразование Лапласа означает переход от функции F(p) к функции f(t) с помощью формулы

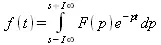
Для вычисления этого интеграла служит функция

invlaplace(expr, р, t)

где expr — выражение относительно переменной p, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение, а обратное — оригинал функции. Ниже приведены примеры определения и применения прямого и обратного преобразований Лапласа:

> restart:with(inttrans):

> convert(laplace(f(t),t,s), int);

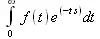
> laplace(sin(t)+a*cos(t),t,p);

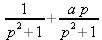
> invlaplace(%,р,t);

Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t)+a cos(t). Преобразования Лапласа широко используются со специальными функциями и, в свою очередь, порождают специальные функции:

> laplace(FresnelC(t),t,p);

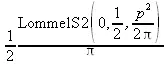
> laplace(Si(t)+Ci(t)+erf(t),t,p);

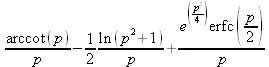
> laplace(BesselJ(0,t),t,p);

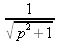
> invlaplace(1/sqr(р^2+1),t,р);

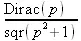
Преобразования Лапласа широко используются для решения линейных дифференциальных уравнений в аналитическом виде. Ниже дана пара простых примеров, иллюстрирующих технику такого решения для дифференциальных уравнений второго порядка с применением функции dsolve:

> de1 := diff(y(t),t$2) + 2*diff(y(t),t) + 3*y(t) = 0;