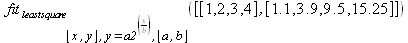Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Применение регрессии обычно оправдано при достаточно большом числе точек исходных данных. При этом регрессия может использоваться для сглаживания данных.

Функция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных

> f:=fit[leastsquare[[x, у, z],z=a+b*x+c*y,{a,b,c}]]\

([[1,2,3,5,5], [2,4,6,8,8], [3, 5, 7,10, Weight (15, 2)]]) ;

> fa:=unapply(rhs(f),x,у);

> fa(l., 2.) ;

> fa(2,3);

В данном случае уравнение регрессии задано в виде z = а + bх + су. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в невычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у.

Функция fit может использоваться и для выполнения линейной регрессии общего вида:

Функция такой регрессии является линейной комбинацией ряда функций f1(х), f2(х), f3(х), причем каждая их них может быть и нелинейной, например экспоненциальной, логарифмической, тригонометрической и т.д. Пример линейной регрессии общего вида представлен на рис. 5.30.

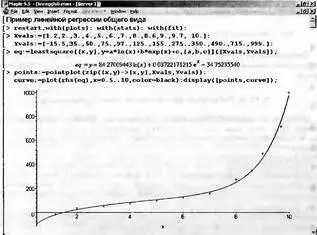
Рис. 5.30. Пример выполнения линейной регрессии общего вида

В литературе и даже в документах системы Maple линейная регрессия общего вида часто называется нелинейной регрессий. Однако это неверно, поскольку нелинейной является регрессия, функция которой не может быть представлена линейной комбинацией функций.

К сожалению, функция fit неприменима для нелинейной регрессии. При попытке ее проведения возвращается структура процедуры, но не результат регрессии — см. пример ниже:

> fit[leastsquare[[х,у], у=а*2^(х/b),{а,b}]]([[1,2,3,4], [1.1,3.9,9.5,15.25]]);

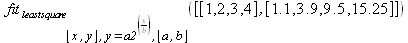
Однако, большинство нелинейных зависимостей удается свести к линейным с помощью простых линеаризирующих преобразований [1, 2, 4]. На рис. 5.31 показан пример экспоненциальной регрессии f(x)=ае bх , которая (благодаря логарифмированию точек y) сводится к линейной регрессии. Детали преобразований даны в документе рис. 5.31. Используя другие преобразования этот документ легко приспособить для выполнения других видов нелинейной регрессии, например степенной или логарифмической.

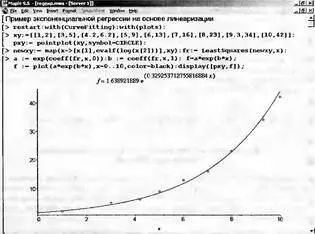
Рис. 5.31. Пример экспоненциальной регрессии

Функция нелинейной регрессии входит в новейший пакет оптимизации Optimization, введенный в Maple 9.5, и описанный в следующей главе. Кроме того, на Интернет-сайте корпорации Waterloo Maple можно найти файлы simplenl.mws и gennlr.mws с процедурами и примерами линейной и нелинейной регрессий общего вида. Интересная реализация нелинейной регрессии для кусочной функции дается в файле nonelinearpiecewise.mws.

Функция BSplineCurve из пакета CurveFitting может использоваться для реализации сплайновой регрессии. Пример этого представлен на рис. 5.32. Опция order задает порядок B-сплайнов, который на 1 меньше заданного целого значения.

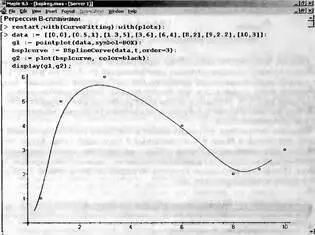
Рис. 5.32. Пример выполнения сплайновой регрессии В-сплайнами

Функция BsplineCurve выглядит несколько недоделанной. Так, при order=3 и 4 кривая регрессии не дотягивает до концевых точек, а при установки order=1 все точки соединяются отрезками прямых — в том числе концевые. Так что использовать эту функцию для экстраполяции нельзя.