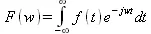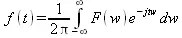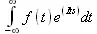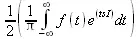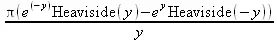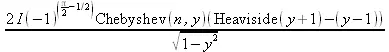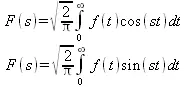> х := array([1.,2.,3.,4.]): у := array([5.,6.,7.,8.]):
> FFT(2,х,y);
4
> print(х);
[10., -4., -2., 0.]
> print(y);
[26., 0., -2., -4.]
> iFFT(2,х,y);
4
> print(x);
[1.0000000, 2.0000000, 3.0000000, 4.0000000]
> print(y);
[5.0000000, 6.0000000, 7.0000000, 8.0000000]
Несмотря на высокую эффективность быстрых преобразований Фурье их недостатком является применение только к дискретно заданным численным данным, причем с числом отсчетов кратным двум в целой степени. Если данных меньше, недостающие элементы обычно заменяются нулями.
Альтернативой преобразований Фурье в наши дни стали вейвлет-преобразования. Вейвлеты это новый обширный базис для приближения произвольных зависимостей вейвлетами — «короткими» волночками разной формы, способными к масштабированию и перемещению. Вейвлеты прекрасно подходят для приближения локальных особенностей различных зависимостей, в том числе нестационарных (с параметрами, меняющимися во времени). Ознакомиться с вейвлетами и средствами работы с ними в системах MATLAB, Mathematica и Mathcad можно по книге [55]. К сожалению, в Maple готовые средства вейвлет-преобразований отсутствуют и это серьезный недостаток этих систем.
5.11.3. Общая характеристика пакета inttrans
Для расширенной поддержки интегральных преобразований служит пакет inttrans
Это один из пакетов, наиболее важных для общематематических и научно-технических приложений. Он вызывается командой
> with(inttrans);
[addtable, fourier, fouriercos, fouriersin, hankel, hilbert, invfourier, invhilbert, invlaplace, invmellin, laplace, mellin, savetable]
и содержит небольшой набор функций. Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье и ряд других интегральных преобразований. Ниже они обсуждены более подробно.
5.11.4. Прямое и обратное преобразование Фурье
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот F(w) и заключается в вычислении следующей интегральной функции:
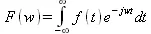
Оно в аналитическом виде реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr, t, w)
Здесь expr — выражение (уравнение или множество), t — переменная, от которой зависит expr, и w — переменная, относительно которой записывается результирующая функция.
Обратное преобразование Фурье задается вычислением интеграла
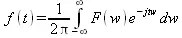
Оно фактически переводит представление сигнала из частотной области во временную. Благодаря этому преобразования Фурье удобны для анализа прохождения воздействий (сигналов) si(t) через устройства (цепи), заданные их частотной характеристикой K(w):
si(t)→fourier→s(w)→s(w)∙K(w)→invfourier→so(t).
Здесь si(t) и so(t) — временные зависимости соответственно входного и выходного сигналов.
Определение (визуализация) преобразований Фурье и примеры их осуществления представлены ниже:
> restart:with(inttrans): assume(lambda>0,а>0):
> convert(fourier(f(t), t, s), int);
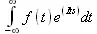
> convert(invfourier(f(t),t,s),int);
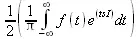
> fourier(sin(t),t,w);
-I π Dirac(w - 1) + I π Dirac(w + 1)
> invfourier(%,w,t);
sin(t)
> fourier(1-exp(-a*t),t,w);
2 π Dirac(w) - fourier(e (-at),t,w)
> invfourier(%,w,t);
1 - e (-at)
> fourier(ln(1/sqrt(1+x^2)),x,y);
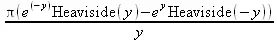
> fourier(BesselJ(n,x),x,y);
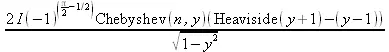
5.11.5. Вычисление косинусного и синусного интегралов Фурье
Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:
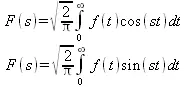
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция f(t).
Читать дальше
Конец ознакомительного отрывка
Купить книгу