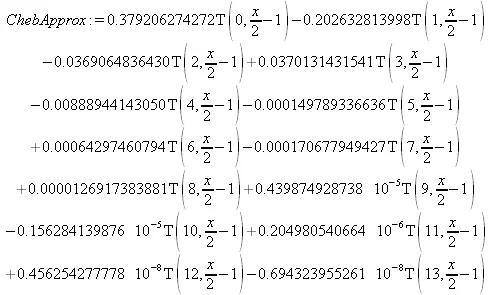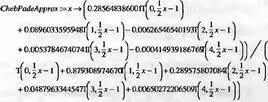Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Разложим функцию f(x) на [0,4] в ряд Чебышева с точностью 1*10 -8. Это означает, что все члены с коэффициентами меньше, чем эта величина, будут опущены. Такая точность обеспечивается полиномом 13 степени:

> evalf(limit(f(x), х=0));

> fproc := proc(x) if x=0 then 0.5 else evalf(f(x)) fi end:

> ChebApprox := chebyshev(fproc, x=0..4, 1E-8);

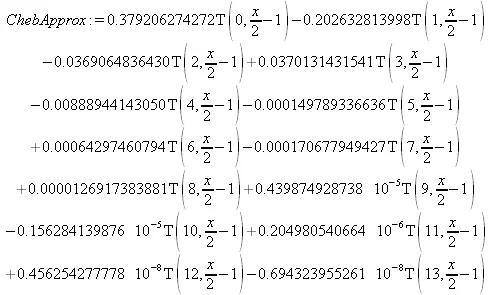
Можно проверить для этого примера, что кривая ошибки при аппроксимации рядом Чебышева колеблется. Поскольку ряд Чебышева был оборван на члене степени 8 (как и полином ряда Тейлора), то максимальная ошибка оказалась все еще больше заданной.

Для последующих вычислений, полезно заметить, что мы можем использовать процедуру для нахождения численных значений f(x), которая будет намного эффективнее, чем прямое определение, которое требует численного интегрирования для каждого значения х. А именно, определим процедуру численной оценки, основанную на разложении в ряд Чебышева степени 13, так как максимальная ошибка при такой аппроксимации меньше, чем 10 -8, и обеспечивает для нашей цели достаточную точность. Мы определим полином Чебышева Т(х) из пакета orthopoly, и затем для эффективной оценки преобразуем его в форму Горнера:

> F := hornerform(eval(subs(T=orthopoly[T],

ChebApprox)));

> F := unapply(F, x):

Схема Горнера минимизирует число арифметических операций, заменяя операции возведения в степень операциями последовательного умножения.

Теперь рассмотрим еще более точную рациональную аппроксимацию Чебышева-Паде. Это такая рациональная функция r[m, n](х) с числителем степени m и знаменателем степени n такой же, как и для разложения в ряд Чебышева. Функция r[m, n](х) согласуется с разложения в ряд ряда Чебышева f(x) членом степени m+n. Мы вычислим аппроксимацию Чебышева-Паде степени (4, 4), подобную обычной Паде-аппроксимации, успешно выполненной ранее:

> ChebPadeApprox := chebpade(F, 0..4, [4,4]);

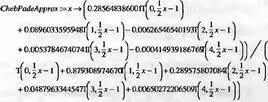
Построим кривую ошибок:

> with(orthopoly, Т):

> plot(F - ChebPadeApprox, 0..4,color=black);

Она представлена на рис. 5.27.

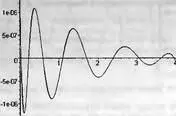
Рис. 5.27. Кривая ошибки при Паде-Чебышева рациональной аппроксимации

Максимальная ошибка и на этот раз имеет место в левой оконечной точке. Величина максимальной ошибки несколько меньше, чем ошибка при аппроксимации рядом Чебышева. Главное преимущество преставления в виде рациональной функции — высокая эффективность вычислений, которая может быть достигнута преобразованием в непрерывную (цепную) дробь (см. ниже). Однако полученная максимальная ошибка чуть-чуть больше заданной:

> maxChebPadeError := abs(F(0) - ChebPadeApprox(0));

Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации.

Классический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (m, n) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax:

> MinimaxApprox := minimax(F, 0..4, [4,4], 1, 'maxerror');

Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы, наконец, достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10 -6:

> maxMinimaxError := maxerror;

Построим график погрешности для данного типа аппроксимации: