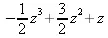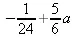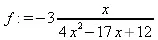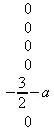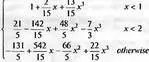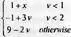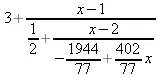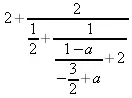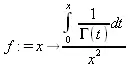5.9.7. Функция полиномиальной аппроксимации
Функция Polynomial Interpolation реализует полиномиальную интерполяцию и может использоваться в виде:
PolynomialInterpolation(xydata, v)
PolynomialInterpolation(xdata, ydata, v)
Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже
> with(CurveFitting):
PolynomialInterpolation([[0,0], [1,2], [2,4], [3, 3]], z);
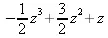
> PolynomialInterpolation([0, 2, 5, 8], [2, a, 1, 3], 3);
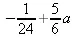
5.9.8. Функция рациональной аппроксимации
Функция рациональной интерполяции задается в виде:
RationalInterpolation(xydata, z, opts)
RationalInterpolation(xdata, ydata, z, opts)
где необязательный параметр opts задается выражениями method=methodtype или degrees=[d1,d2]. Функция возвращает результат в виде отношения двух полиномов.
Параметр methodtype может иметь значения lookaround или subresultant, задающие учет или пропуск сингулярных точек.
Пример применения функции RationalInterpolation (загрузка пакета опущена, но предполагается):
> xpoints := [0,1,2,3,4,-1]: ypoints := [0, 3, 1, 3, а, 1/11]:
f := RationalInterpolation(xpoints, ypoints, x);
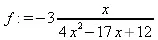
> for i from 1 to 6 do normal(eval(f,x=xpoints[i])-ypoints[i]) end do;
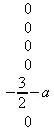
5.9.9. Функция вычисления обычных сплайнов Spline
Функция
Spline(xydata, v, opts)
Spline(xdata, ydata, v, opts)
вычисляет обычные (не В-типа) сплайны. Примеры ее применения даны ниже:
> Spline([[0,1], [1,2], [2,5], [3,3]], х);
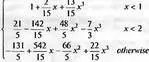
> Spline([0,1,2,3], [1,2,5,3], v, degree=1);
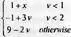
5.9.10. Функция аппроксимации непрерывными дробями
Функция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's — интерполяцию). Она задается в виде:
ThieleInterpolation(xydata, v)
ThieleInterpolation(xdata, ydata, v)
Примеры применения данной функции представлены ниже:
> ThieleInterpolation([[1,3],[2,5],[4,75],[5,4]], х);
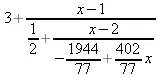
> ThieleInterpolation([1,2,а], [2,4,3], 3)
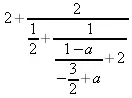
5.10. Выбор аппроксимации для сложной функции
5.10.1. Задание исходной функции и построение ее графика
Трудно представить себе область научно-технических расчетов более широкую и почитаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом систем Maple на одном из комплексных примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанном для Maple 9.5/10. В этом примере используются многие из описанных выше средств приближения функций.
Воспользуемся ранее описанными возможностями пакета numapprox, для чего, прежде всего, подключим его:
> restart:with(numapprox):
Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции:
> f := х -> int(1/GAMMA(t), t=0..x ) / х^2;
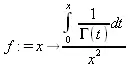
> plot(f,0..4,color=black);
График этой функции представлен на рис. 5.24. С первого взгляда это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу заметите, что график строится медленно, поскольку в каждой из множества его точек системе Maple приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма-функцию. И делает это Maple по сложному и медленному алгоритму адаптивного численного интегрирования.
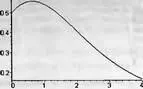
Рис. 5.24. График аппроксимируемой функции
Читать дальше
Конец ознакомительного отрывка
Купить книгу