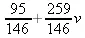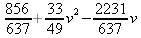Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Однако если точки данных расположены неравномерно, то применение полиномиальной аппроксимации может оказаться совершенно неприемлемым. Это отчетливо показывает пример, представленный на рис. 5.20. Здесь задана на первый взгляд (судя по расположению точек) не слишком сложная и чуть колебательная зависимость. Однако полиномиальная аппроксимация (представлена тонкой кривой), особенно в начале — в интервале первых трех точек, дает явно ошибочные сильные выбросы. А вот сплайновая аппроксимация (показана более жирном линией) ведет себя куда более приемлемо.

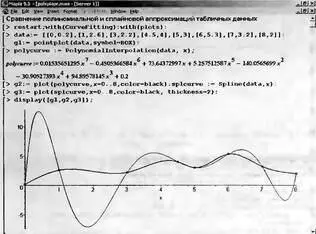
Рис. 5.20. Сравнение полиномиальной и сплайновой аппроксимаций для функции, заданной парами данных при неравномерном расположении узлов

Причина лучшего поведения сплайновой аппроксимации здесь вполне очевидна — напоминая поведение гибкой линейки, сплайновая функция эффективно сглаживает выбросы кривой в промежутках между точками.

При большом числе узлов (десятки-сотни и выше) данные представленные точками выглядят нередко не представительно. Например, на рис. 5.21 показан документ, иллюстрирующий сплайновую аппроксимацию функции синуса, представленной 31 отсчетом, но без вывода графика сплайновой функции. Несмотря на равномерное расположение узлов по графику точек невозможно определить, что это функция синуса.

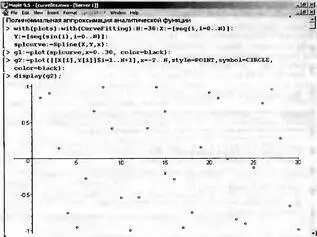
Рис. 5.21 Пример представления функции синуса 31 узловыми точками при равномерном расположении узлов

Рисунок 5.22 отличается от рис. 5.21 только построением сплайновой функции, представленной графическим объектом g1 (на рис. 5.19 он исключен из параметров функции display). После построения графика сплайновой аппроксимирующей функции становится вполне ясным, что точки представляют функцию синуса, которая прекрасно представляется отрезками полиномов сплайн-функции.

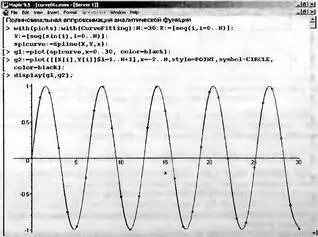
Рис. 5.22. Пример сплайновой аппроксимации синусоидальной функции

Здесь полезно обратить внимание на то, что за пределами области узловых точек значения, возвращаемые сплайновой функцией в пакете CurveFitting равны нулю. Так что экстраполяция по ней невозможна (в тоже время функция spline такой возможностью обладает).

До сих пор мы рассматривали методы числовой аппроксимации функций или данных, при которых порядок полиномов определялся числом отсчетов функции.

Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов. При этом методе происходит статистическая обработка данных (самих по себе или представляющих функцию) исходя из минимума среднеквадратической погрешности для всех отсчетов. Эта функция реализуется в формах:

LeastSquares(xydata, v, opts)

LeastSquares(xdata, ydata, v, opts)

Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset.

Следующие примеры иллюстрируют применение функции LeastSquares:

> with(CurveFitting):

LeastSquares([[0,.5], [1,2], [2,4], [3,8]], v);

> LeastSquares([0,1,2,3], [1,2,4,6], v, weight-[1,1,1,10]);

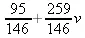
> LeastSquares([0,1,3,5,6], [1,-1,-3,0,5], v, curve=a*v^2+k*v+c);

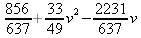
Наглядную иллюстрацию приближения группы точек кривой (в данном случае представленной полиномом четвертой степени) дает рис. 5.23. Кривая в облаке точек располагается таким образом, что площади квадратов над кривой и под ней в сумме равны нулю.

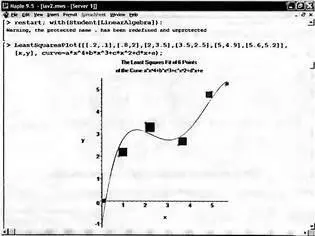
Рис. 5.23. Графическое представление метода наименьших квадратов

В конце этой главы мы вернемся к реализации метода наименьших квадратов при выполнении регрессионного анализа, построенного па этом методе.