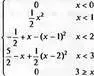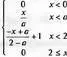Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):

> Digits:=12:w:=proc(х) 1.0 end;

> f:=proc(x) evalf(erf(x)) end;

> crit:=array(1..7, [0, .1,.25,.5,.75,.9,1.]);

> remez(w,f,0,1,5,0,crit,'maxerror');

> maxerror;

Отметим назначение других функций пакета numapprox:

chebdeg(p) — возвращает степень полинома Чебышева р;

chebmult(p, q) — умножение полиномов Чебышева p и q;

chebsort(e) — сортирует элементы ряда Чебышева;

confracform(r) — преобразует рациональное выражение r в цепную дробь;

confracform(r, х) — преобразует рациональное выражение r в цепную дробь с независимой переменной х;

hornerform(r) — преобразует рациональное выражение r в форму Горнера;

hornerform(r, х) — преобразует рациональное выражение r в форму Горнера с независимой переменной х;

infnorm(f, x=a…b, 'xmax') — возвращает L-бесконечную норму функции на отрезке х[а, b];

infnorm(f, a…b, "xmax") — возвращает L-бесконечную норму функции на отрезке [ а, b ].

Действие этих функций очевидно и читатель может самостоятельно опробовать их в работе.

Появившийся еще в Maple 7 пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций:

> with(CurveFitting);

Доступ к функциям пакета возможен с помощью конструкций:

CurveFitting[function](arguments) function(arguments)

Число функций пакета невелико и все они описаны ниже.

Функция BSpline(k, v, opt) служит для вычисления В-сплайнов. В отличии от обычных сплайнов, у которых точками стыковки сплайн-функций являются узловые точки, В-сплайны позволяют получить стыковку в произвольно заданных точках. Указанная функция имеет следующие параметры: k — порядок сплайна (целое число), v — имя и opt — параметр в виде knots=knotlist, где knotlist — список из k+ 1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve] можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже:

> BSpline(3, х);

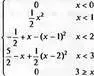
> BSpline(2, х, knots=[0,a,2]);

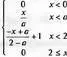
Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise.

Функция BsplineCurve служит для построения кривых B-сплайнов. Она может использоваться в формах:

BSplineCurve(xydata, v, opts)

BSplineCurve(xdata, ydata, v, opts)

Здесь:

xydata — список, массив или матрица точек в форме [[х1,у1],[х2,у2],…,[хn,уn]];

xdata — список, массив или вектор значений независимой переменной [х1,х2,…,хn];

ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,…,уn];

v — имя независимой переменной;

opts — не обязательный параметр в форме одного или более выражений вида order=k или knots=knotlist.

Примеры применения функции BSplineCurve с порядком, заданным по умолчанию и с третьим порядком (кубический B-сплайн), представлены на рис. 5.19.

Следует отметить, что при малом числе точек стыковки аппроксимация B-сплайнами дает невысокую точность, что хорошо видно из рис. 5.19.

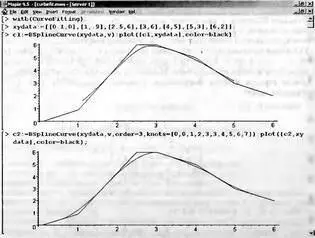
Рис. 5.19. Применение функции BSplineCurve

Когда аппроксимируется гладкая функция, представленная парами данных с равномерным расположением узлом, то данные как полиномиальной, так и сплайновой аппроксимаций различаются незначительно. В этом случае применение куда более сложной сплайновой аппроксимации, как правило, кажется мало обоснованным.