Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

В ходе решения задач линейной алгебры часто приходится использовать различные методы, например известный еще из школы метод исключения Гаусса. Однако для эффективного решения таких задач приходится представлять матрицы специальным образом, осуществляя матричные разложения. В ходе этого приходится работать с некоторыми специальными типами матриц, что нередко резко упрощает решения систем линейных уравнений. Отметим некоторые из наиболее распространенных матричных разложений, которые реализованы в большинстве СКА и СКМ.

LU-разложение, называемое также треугольным разложением, соответствует матричному выражению вида Р∙А= L∙U, где L— нижняя и U— верхняя треугольные матрицы. Все матрицы в этом выражении квадратные.

QR-разложение имеет вид А= Q∙R, где Q— ортогональная матрица, a R— верхняя треугольная матрица. Это разложение часто используется при решении любых систем линейных уравнений, в том числе переопределенных и недоопределенных и с прямоугольной матрицей.

Разложение Холецкого А= L∙L T применяется к симметричной матрице А, при этом L— треугольная матрица.

Сингулярное разложение матрицы Аразмера M×N (М×N) определяется выражением А= U∙s∙VT, где Uи V— ортогональные матрицы размера N×N и М×M , соответственно, a s— диагональная матрица с сингулярными числами матрицы Ана диагонали.

Элементы векторов и матриц в Maple являются индексированными переменными, то есть место каждого элемента вектора определяется его индексом, а у матрицы — двумя индексами. Обычно их обобщенно обозначают как i (номер строки матрицы или порядковый номер элемента вектора) и j (номер столбца матрицы). Допустимы операции вызова нужного элемента и присваивания ему нового значения:

V[i] — вызов i-го элемента вектора V;

M[i,j] — вызов элемента матрицы М, расположенного на i -й строке в j- м столбце.

V[i]:=x — присваивание нового значения х i-му элементу вектора V;

M[i,j]:=x — присваивание нового значения х элементу матрицы М.

Прежде всего, надо обратить внимание на то, что векторы и матрицы, хотя и похожи на списки, но не полностью отождествляются с ними. В этом можно убедиться с помощью следующих примеров (файл vmop), в которых функция type используется для контроля типов множественных объектов (векторов и матриц):

> М1:=[1,2,3,4];

> type(M1,vector);

> V:=convert(M1,vector);

> type(V,vector);

> М2:=[[1,2],[3,4]];

> type(М2,matrix);

> M:=convert(M2,matrix);

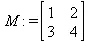
> type(M,matrix);

Таким образом, используя функцию преобразования данных convert, можно преобразовывать одномерные списки в векторы, а двумерные — в матрицы. Функция type используется в следующих формах:

type(V,vector) — тестирует аргумент V и возвращает true, если V — вектор, и false в ином случае;

type(M.matrix) — тестирует аргумент М и возвращает true, если М — матрица, и false в ином случае.

Здесь параметры vector и matrix используются для указания того, какой тип объекта проверяется. Обратите внимание на то, что матрицы отображаются иначе, чем двумерные списки — без двойных квадратных скобок. Отображение вектора подобно отображению одномерного списка, поэтому здесь особенно важен контроль типов данных.

Важное достоинство систем компьютерной алгебры, к которым относится и Maple, заключается в возможности выполнения аналитических (символьных) операций над векторами и матрицами. Перед проведением символьных операций с векторами и матрицами рекомендуется очистить память от предшествующих определений с помощью команды restart. Если какие-то элементы векторов или матриц были ранее определены, это может привести к очень сильным искажениям вида конечных результатов. Очистка памяти устраняет возможность ошибок такого рода.