К недостаткам этой формы записи можно отнести то, что с изменением числа узлов необходимо все вычисления проводить заново. Выражение (5.4) можно записать в более компактной форме:
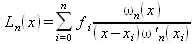 (5.5)
(5.5)
Теоретически максимальную точность обеспечивает полином высокой степени. Однако на практике часто используется полином невысокой степени (линейная и квадратичная интерполяция) с увеличением степени интерполяционного полинома возрастают колебательные свойства полинома. Аппроксимация с помощью интерполяционного полинома Лагранжа является достаточно эффективной, когда интерполируются гладкие функции и число n является малым. В частности в математическом обеспечении компьютерных средств имеется стандартные подпрограммы аппроксимации, в которых реализована формула Лагранжа.
5.6.4. Интерполяционный метод Ньютона
На практике для повышения точности интерполяционного полинома незначительно увеличивают количество узлов интерполяции. В этом случае использование метода Лагранжа неудобно, так как добавление дополнительных узлов приводит необходимости пересчета всего интерполяционного полинома в целом. Эти недостатки устраняются, если записать полином Лагранжа, используя интерполяционный метод Ньютона.
Используя понятия разделенных разностей для полинома Ньютона можно получить выражение:
N n(x) = f(x 0) + (x-x 0)f(x 1, x 0) + (x-x 0)(x-x 1)f(x 0, x 1, x 2) + … + (x-x 0)(x-x 1)…(x-x n)f(x, x 0, x 1, …, x n) (5.6)
Представление интерполяционного полинома в форме Ньютона является более удобным в практических расчетах. На практике часто заранее неизвестно количество узлов и, следовательно, степень интерполяционного полинома. Для повышения точности интерполяции в сумму могут быть добавлены новые члены, что требует подключение новых узлов. Добавление новых узлов интерполяции приводит лишь к появлению новых слагаемых полинома, без изменения уже существующих, что не требует пересчета всех коэффициентов заново. При добавлении новых узлов интерполяции неважно, в каком порядке они подключаются, но существует одно условие — узлы х, не должны совпадать.
5.6.5. Итерационно-интерполяционный метод Эйткена
Итерационно-интерполяционный метод Эйткена позволяет свести вычисления коэффициентов интерполяционного полинома Лагранжа, с учетом его равенства в узлах интерполяции с исходными данными к вычислению функциональных определителей второго порядка. При этом эффективность метода повышается в тех случаях, когда нет необходимости в получении приближенного аналитического выражения функции f(х), заданной таблично, а требуется лишь определить значение в некоторой точке х*, отличной от узловых точек. Этот метод заключается в последовательной линейной интерполяции. Процесс вычисления f(x*) состоит в следующем: необходимо пронумеровать узлы интерполяции, например, в порядке убывания их от х*. Затем для каждой узловой точки интерполяции строятся соотношения:
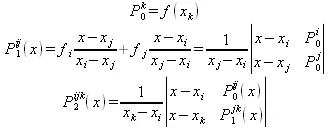
которые является интерполяционными полиномами, построенными соответственно по узлам х i , х j , х k . Продолжая этот процесс, имеем следующий полином:
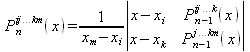 (5.7)
(5.7)
Полученный полином является интерполяционным полиномом, построенный по узлам х i , x j , …, х k , х m . Это утверждение верное, так как Р n-1 ij…k (х) и Р n-1 j…km (x) являются интерполяционными полиномами. При его реализации предполагается, что функция гладкая, а также критерием оценки погрешности определяется некоторое значение, определяемое условиями конкретной задачи.
5.6.6. Чебышевская интерполяция
Метод Чебышева был создан для оптимального выбора узлов интерполяции, если это возможно при решении конкретной задачи, и для получения минимально возможной погрешности аппроксимации. Предполагается, что в выборе расположения узлов интерполяции ограничений нет, и предполагается, что узлы выбираются произвольно. Ставится задача о наилучшем выборе узлов. Наилучшими узлами х, следует признать те, для которых выражение max [a,b]|ω n(x)| минимально для рассматриваемого класса функций (алгебраических полиномов). Определение этих узлов сводится к нахождению корней полинома, наименее уклоняющихся от нуля на [a, b]. Такой полином порождается полиномом Чебышева первого рода T n+1.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

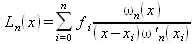 (5.5)
(5.5)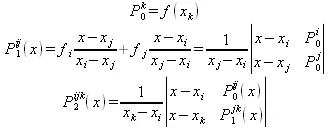
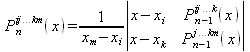 (5.7)
(5.7)










