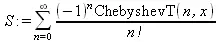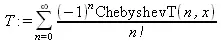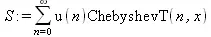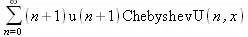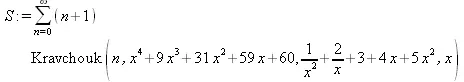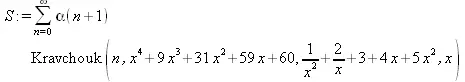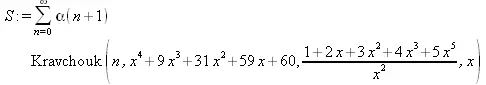> OrthogonalSeries[Create](u(n),HermiteH(n,x));

В другом примере показано представление полиномиального выражения в новом базисе с ортогональными многочленами Чебышева с помощью функции ChangeBasis:
> OrthogonalSeries[ChangeBasis](1+3*у*х^2+у^3*х,
ChebyshevT(n,х), ChebyshevU(m, y));
1 + ¾ChebyshevT(2, x) ChebyshevU(1, y) + ¾ChebyshevU(1, y) + ½ChebyshevT(1, x) ChebyshevU(1, y)
> OrthogonalSeries[Evaluate](%);
3x²y + yx + 1
Обратите внимание на то, что новое выражение после исполнения команды Evaluate приняло вид исходного выражения.
Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору:
> S:=Create((-1)^n/n!, ChebyshevT(n, х));
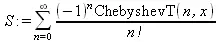
> Т:=Сору(S);
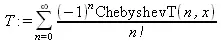
Вычисление производной от ряда с ортогональными многочленами представлено ниже:
> S := Create(u(n),ChebyshevT(n,х));
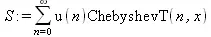
> Derivate(S, х);
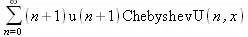
Еще один пример демонстрирует операцию скалярного умножения ряда с помощью функции ScalarMultiply:
> S := Create(n+1,Kravchouk(n,p,q,x));
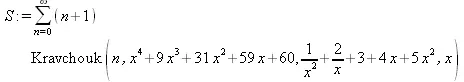
> ScalarMultiply(alpha, S);
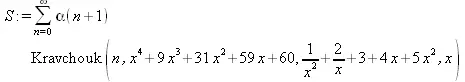
> simplify(%);
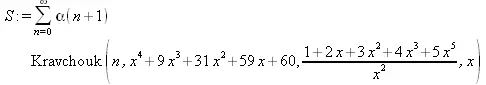
5.5. Пакет PolynomialTools
5.5.1. Обзор возможностей пакета PolynomialTools
Для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами служит пакет PolynomialTools. Этот пакет имеет небольшое число функций:
> with(PolynomialTools);
[CoefficientList, CoefficientVector, Hurwitz, IsSelfReciprocal, MinimalPolynomial , PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate]
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
5.5.2. Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера.
Функция IsSelfReciprocal(a, х, 'р') — проверяет полином а(х) на условие соeff(a,x,k)=coeff(a,x,d-k) для всех k=0..d, где d=degree(a, х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином P порядка d/2, такой, что x^(d/2)*P(x+1/x)=а. При нечетном d, полином а будет взаимо-обратным, что подразумевает деление на х+1. В этом случае если p указано, результат вычисляется в форме а/(х+1).
Примеры применения этой функции представлены ниже (файл poltools):
> with(PolynomialTools):
IsSelfReciprocal(х^4+х^3+х+1, x, 'p');
true
> p;
-2 + x + x²
> IsSelfReciprocal(х^5-3*х^4+х^3+х^2-3*х+1, x, 'p');
true
> p;
3-4x+x²
> r := evalf(1+sqrt(2));
r := 2.414213562
Функция MinimalPolynomial(r, n, acc) возвращает полином минимальной степени не превышающей n, имеющий корень r. Необязательный аргумент acc задает погрешность приближения. Функция MinimalPolynomial(r, n) использует решетчатый алгоритм и находит полином степени n (или менее) с наименьшими целыми коэффициентами. Корень r может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию acc задано как 10^(Digits-2). Примеры применения данной функции:
> MinimalPolynomial(r, 2);
-1 - 2_Х + _Х²
> r := 1+sqrt(2);
r:= 1 + √2
> ( r, 2 );
1+√2, 2
> MinimalPolynomial( 1.234, 3 );
-109 + 61_Х - 5_Х² + 22_ X³
> fsolve( %, X );
Читать дальше
Конец ознакомительного отрывка
Купить книгу