Здесь мы будем рассматривать такие виды аппроксимации, которые дают точные значения функции y(x) в узловых точках в пределах погрешности вычислений по умолчанию. Если аппроксимирующая зависимость выбирается из условия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов.
5.6.2. Полиномиальная аппроксимация и интерполяция аналитических зависимостей
Рассмотрим основы полиномиальной аппроксимации (приближения) функциональных зависимостей. Пусть приближаемая функция φ(х) должна совпадать с исходной функцией f(х) в (n+1)-точке, то есть должно выполняться равенство: φ(х i)=f(х i)=f i, i = 0, …, n. В качестве приближающей функции примем алгебраический полином:
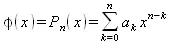 (5.1)
(5.1)
Выбор конкретного значения n во многом определяется свойствами приближающей функции, требуемой точностью, а также выбором узлов интерполяции. В случае аналитической функциональной зависимости выбор степени полинома может быть любым и чаще всего определяется компромиссом между сложностью полинома, скоростью его вычисления и погрешностью. В качестве критерия согласия принимается условия совпадения функций f и q в узловых точках:
f(х i) = Р n(х i), (i=0, 1, … n ). (5.2)
Полином Р n (х) удовлетворяющий данному условию будет интерполяционным полиномом.
Для задачи интерполирования в интервале [a, b] выбираются значения аргументов а≤х 0 1 <���…<���х n ≤b, которые соответствуют значениям f i=f(х i) (i=0, 1, ..., n ) функции f. Для этой функции будет существовать и притом единственный полином степени не выше n, который принимает в узлах х, заданные значения f i . Для нахождения этого полинома решается система алгебраических уравнений
а 0х t n+a 1х t n-1+ ... +а n= f i, (i=0, 1, ..., n).
Подставив полученные значения a_k в равенство (5.1) можно получить обобщенную форму представления интерполяционного полинома
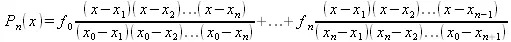 (5.3)
(5.3)
Получив интерполяционный полином (5.3), необходимо выяснить, насколько близко он приближается к исходной функции в других точках отрезка [a, b]. Обычно для этого строится график f(x) и Р n (х) и график их разности, т. е. абсолютной погрешности. Последняя определяется выражением:
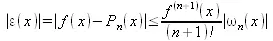 (5.4)
(5.4)
Вопреки существующему мнению о быстрой потери точности полиномиальной аппроксимации при n>(5–7) погрешность ее быстро уменьшается при увеличении n. Но это только при условии, что все вычисления выполняются точно! При выборе метода приближения необходимо обеспечить по возможности более высокую точность приближения и одновременно простоту построения φ(х) по имеющейся информации о приближаемой функции f(х).
5.6.3. Интерполяционный метод Лагранжа.
При решении практических задач часто используют специальные виды интерполяционных полиномов, которые упрощают некоторые вычислительные процедуры. Данный метод предполагает введение вспомогательного полинома l i(х) степени n. Полином l i(х) в точке х, должен быть равен 1, а в остальных точках отрезка интерполяции должен обращаться в нуль.
Удовлетворяющий этому полином может быть представлен в виде:
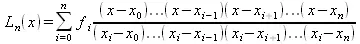 (5.5)
(5.5)
Это выражение известно как интерполяционный полином Лагранжа. Важным достоинством ее является то, что число арифметических операций, необходимых для построения полинома Лагранжа, пропорционально n² и является наименьшим для всех форм записи. Данная форма интерполяционного полинома применима как для равноотстоящих, так и для неравноотстоящих узлов. Достоинством является и то, что интерполяционный полином Лагранжа удобен, когда значения функций меняется, а узлы интерполяции неизменны, что имеет место во многих экспериментальных исследованиях. Рекомендуется использовать запись интерполяционного полинома в форме Лагранжа при теоретических исследованиях при изучении вопроса сходимости L n (f, х) к f при n→∞ .
Читать дальше
Конец ознакомительного отрывка
Купить книгу

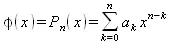 (5.1)
(5.1)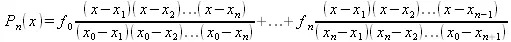 (5.3)
(5.3)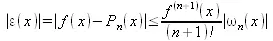 (5.4)
(5.4)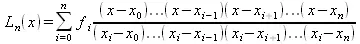 (5.5)
(5.5)










