Полиномы Чебышева определены в интервале [-1,1]. Для перевода интерполяции в интервале [ a, b ], выполняется линейная замена переменной х :
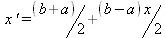
В качестве узлов интерполяции берутся корни полинома Чебышева:
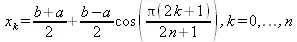 (5.8)
(5.8)
Тогда погрешность Чебышевской интерполяции определяется выражением:
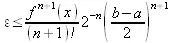 (5.9)
(5.9)
5.6.7. Сплайновая интерполяция, экстраполяция и аппроксимация
Использование одной интерполяционной формулы для большого числа узлов нецелесообразно, так как при этом интерполяционный полином сильно проявляет свои колебательные свойства, и значение между узлами могут сильно отличаться от значений интерполируемой функции. Одна из возможностей преодоления этого недостатка заключается в применении сплайн-интерполяции.
Наиболее известным и широко применяемым является случай сплайновой интерполяции, когда между двумя точками строится полином n-й степени
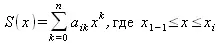 (5.10)
(5.10)
который в узлах интерполяции принимает значения интерполируемой функции и непрерывен вместе со своими (n-1)-ми производными. Такой кусочно-непрерывный интерполяционный полином называется сплайном. Его коэффициенты находят из условий в узлах интерполяции — равенства значений сплайна и приближаемой функции, а также равенства (n- 1)-й производной соответствующих полиномов. Максимальная по всем частичным отрезкам степень полинома является степенью сплайна.
Одним из наиболее распространенных интерполяционных сплайнов является кубический интерполяционный сплайн. Для вывода уравнения кубического интерполяционного сплайна можно воспользоваться его представлением в виде гибкой линейки, изогнутой таким образом, что она проходит через значения функции в узлах, то есть, является упругой рейкой в состоянии равновесия. Это его состояние описывается уравнением S'''(х)=0, где S'''(х) — четвертая производная. Из этого следует, что между каждой парой соседних узлов интерполяционная формула записывается в виде полинома третьей степени. Этот полином удобно представить следующим образом:
S(x) = а i+ b i(x-x i-1) + с(х-х i-1)² + d i(x–х i-1)³, x i-1≤х≤x i, i = 1, 2, ..., n.
Система Maple позволяет легко вычислять коэффициенты кубических полиномов. Метод сплайновой интерполяции дает хорошие результаты при интерполяции непрерывных функций с гладкими производными 1-ой и 2-ой степени. При этом кубическая сплайновая интерполяция, построенная по узлам f i=f(х i), i=0,1,…,n, будет иметь минимум кривизны по сравнению с любой интерполяционной функцией, имеющей непрерывные первую и вторую производные. Выполнение сплайн-интерполяции функций с резким изменением производных дает, как правило, большие ошибки. Сплайны более высоких порядков, чем третий, используется редко, так как при вычислении большого числа коэффициентов может накапливаться ошибка, приводящая к значительным погрешностям.
По сравнению с другими математическими конструкциями сплайны обладают следующими преимуществами: они обладают лучшими аппроксимирующими свойствами, что при равных информационных затратах дает большую точность или равную точность при менее информационных исходных данных. Для увеличения точности часто уменьшают величину шага интерполяции, что увеличивает число узлов. В случае интерполяционных полиномов это связано с возрастанием их степени, что имеет недостатки. Степень же сплайна не изменяется при увеличении количество узлов интерполяции. Это принципиальный момент теории сплайнов.
5.6.8. Рациональная интерполяция и аппроксимация
Большую точность приближения по сравнению полиномиальным приближением можно получить, если исходную функцию заменить, используя рациональную интерполяцию при которой аппроксимирующая функция ищется как отношение двух полиномов. Наиболее важным свойством рациональных функций является то, что ими можно приближать такие функции, которые принимают бесконечные значения для конечных значений аргумента и даже внутри интервала его изменения.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

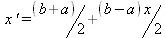
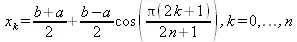 (5.8)
(5.8)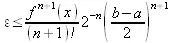 (5.9)
(5.9)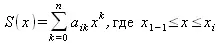 (5.10)
(5.10)










