Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — не обязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {t1, … ,tm}, таких что полином а расщепляется над K=Q(t1, …, tm), где Q означает поле рациональных чисел.

Примеры:

> Split(х^2+х+1,х);

> Split(х^2+у*х+1+у^2, x, 'b');

> b;

В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее.

Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х=х+х0, где х0 — константа. Примеры применения этой функции даны ниже:

> Translate(х^2, х, 1);

> expand(eval(х^2,х=х+1));

> Translate(х^3,х,2);

> expand(eval(х^3,х=х+2));

> Translate((х+1)^3,х,-1);

Для сортировки полиномов предназначены следующие три функции:

Shorter(f, g, х)

Sort(v, х)

Shorten(f, x)

Здесь f и g полиномы, v — список полиномов и x — независимая переменная. Функции отличаются характером сортировки.

Функция Shorter определяет полином f как более короткий, чем g, по следующим признакам: меньшая длина, меньшее имя независимой переменной х, не дробный и меньшая степень других переменных. Функция Sort сортирует лист полиномов х по признакам, определяемым Shorter. Функция Shorten использует преобразования Мёбиуса. Многочисленные детали ее применения можно найти в справке по данной функции. Примеры применения функций сортировки:

> Shorten(х^2+х+1,х);

> Shorten(3*х^3+18*х+14,х);

> Shorten(х^4+32);

> Shorter(х^3,х+5,х);

> Sort([х^3,х^2,х+1,х+5]);

Error, (in sort_poly) sort_poly uses a 2nd argument, x, which is missing

> Sort([х^3,х^2,x+1,x+5],x);

Функция PolynomialToPDE(polys, vars, depvars) преобразует полиномы polys по независимым переменным vars в дифференциальные уравнения с частными производными (PDE). Другая функция PDEToPolynomial(pdes, vars, depvars) осуществляет обратное преобразование. Следующие примеры иллюстрируют применение этих функций:

> S:= PolynomialToPDE([(х^2 - 2*х + 1)*u + x^3*v], [х], [u,v]);

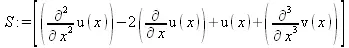
> PDEToPolynomial(S, [х], [u,v]);

Если некоторая зависимость y(х) представлена рядом табличных отсчетов y i(х i), то интерполяцией принято называть вычисление значений y(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [ a, b ], то есть при x и x>b вычисление y(x) называют экстраполяцией (или, иногда, предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(х, у) и даже многомерная интерполяция для функций многих переменных.

Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой, зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна, она эффективна при интерполяции периодических функций.

Аппроксимацией в системах компьютерной математики обычно называют получение приближенных значений какого-либо выражения. Однако под аппроксимацией функциональных зависимостей подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, приближающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы.