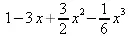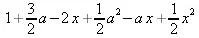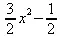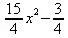Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Отметим определения указанных функций:

G(n,a,x) — полином Гегенбауэра (из семейства ультрасферических полиномов);

H(n,x) — полином Эрмита;

L(n,x) — полином Лагерра;

L(n,a,x) — обобщенный полином Лагерра;

P(n,x) — полином Лежандра;

P(n,a,b,x) — полином Якоби;

T(n,x) — обобщенный полином Чебышева первого рода;

U(n,x) — обобщенный полином Чебышева второго рода.

Свойства ортогональных многочленов хорошо известны. Все они характеризуются целочисленным порядком n, аргументом х и иногда дополнительными параметрами а и b. Существуют простые рекуррентные формулы, позволяющие найти полином n-го порядка по значению полинома (n-1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка.

Ниже представлены примеры вычисления ортогональных полиномов (файл orthpol):

> G(0, 1, х);

> G(1, 1, х);

> G(1, 1, 5);

> Н(3, х);

> L(3, х);

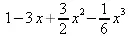
> L(2, а, х);

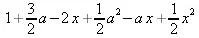
> Р(2, х);

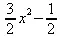
> Р(2, 1, 1, х);

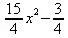
> Т(5, х);

> U(5, х);

В отличие от ряда элементарных функций, ортогональные многочлены определены только для действительного аргумента х. При комплексном аргументе ранее результат просто повторял исходное выражение с многочленом:

> evalf(U(2,2+3*I));

Но уже в Maple 9 ортогональные полиномы с комплексными аргументами могут вычисляться:

> evalf(U(2,2+3*I));

Ортогональные многочлены не определены и для дробного показателя n. Впрочем, надо отметить, что такие многочлены на практике используются крайне редко.

Представляет интерес построение графиков ортогональных многочленов. На рис. 5.6 построены графики ряда многочленов Гегенбауэра и Эрмита. На рис. 5.7 построены графики ортогональных многочленов Лагерра и Лежандра. Наконец на рис. 5.8 даны графики ортогональных многочленов Чебышева T(n , х) и U(n, x) .

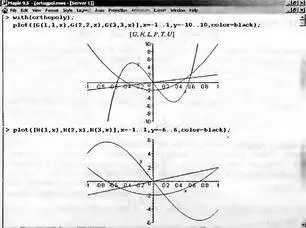
Рис. 5.6. Графики ортогональных многочленов Гегенбауэра и Эрмита

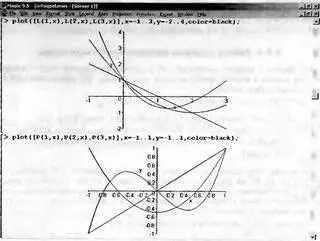
Рис. 5.7. Графики ортогональных многочленов Лагерра и Лежандра

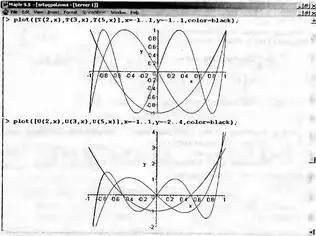
Рис. 5.8. Графики ортогональных многочленов Чебышева

Приведенные графики дают начальное представление о поведении ортогональных многочленов. К примеру, многочлены Чебышева имеют минимальное отклонение от оси абсцисс в заданном интервале изменения х. Это их свойство объясняет полезное применение таких многочленов при решении задач аппроксимации функций, которые рассматриваются в этой главе далее. Можно порекомендовать читателю по их образцу и подобию построить графики ортогональных многочленов при других значения параметра n и диапазонах изменения аргумента х.

Для работы с рядами ортогональных многочленов имеется пакет OrthogonalSeries для работы с рядами ортогональных многочленов. Он имеет довольно представительный набор функций:

> with(OrthogonalSeries);

Поскольку этот пакет представляет интерес, в основном, для опытных математиков, мы не будем рассматривать его функции (в целом достаточно простые) подробно и ограничимся несколькими примерами. В следующем примере с помощью функции Create создается бесконечный ряд с ортогональным многочленом Эрмита в составе базового выражения ряда: