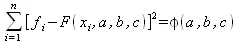 (5.14)
(5.14)
Сумма (5.14) является функцией φ(a, b, с) трех переменных a, b, с. Задача сводится к отысканию ее минимума. Для этого используем необходимое условие экстремума:
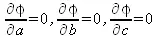
или
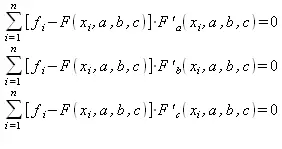 (5.15)
(5.15)
Решив эту систему (5.15) трех уравнений с тремя неизвестными относительно параметров a, b , с, получим конкретный вид искомой функции F(x, a, b, с) . Изменение количества параметров не приведет к изменению сущности метода, а отразится только на количестве уравнений в системе (5.15).
Как следует из начальных условий, найденные значения функции F(x, а, b, с) в точках x 1, х 2, …, х nбудут отличаться от табличных значений y 1 , у 2 , …, у n . Значение разностей
f i-F(x i, a, b, c,) = ε i, i=1, 2, …, n
будет определять отклонение измеренных значений f от вычисленных по формуле (5.14). Для найденной эмпирической формулы (5.14) в соответствии с исходными табличными данными можно найти сумму квадратов отклонений
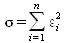 (5.16)
(5.16)
Она, в соответствии с принципом наименьших квадратов для заданного вида приближающей функции и ее найденных параметров (параметры a, b, с ), должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя принципу наименьших квадратов, лучшим нужно считать тот, для которого сумма (5.16) имеет меньшее значение.
5.6.10. Тригонометрическая интерполяция рядами Фурье
При тригонометрической интерполяции используются тригонометрические полиномы — линейные комбинации тригонометрических функций sin(nx) и cos(nx). Этот вид интерполирования применяется для процессов, которые отражают циклические процессы, связанные с периодическими функциями [52–54]. Известно, что такие функции удобно представлять в виде тригонометрического ряда или его частичной суммы с достаточной степенью точности.
Функциональный ряд вида
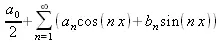 (5.17)
(5.17)
называется тригонометрическим. Его коэффициенты а n и b n — действительные числа, не зависящие от х. Если этот ряд сходится для любого х из промежутка [-π, π], тогда он определяет периодическую функцию f(x) с периодом Т=2π. Ряд вида (5.17) называется рядом Фурье для интегрируемой на отрезке [-π, π] функции f(х), если коэффициенты его вычисляются по следующим правилам:
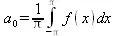 (5.18)
(5.18)
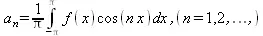 (5.19)
(5.19)
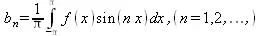 (5.20)
(5.20)
В практических расчетах, как правило, ограничиваются конечным числом первых членов ряда Фурье. В результате получается приближенное аналитическое выражение для функции f(х) в виде тригонометрического полинома N- го порядка
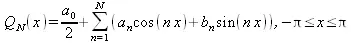
Но соотношения для вычисления коэффициентов Фурье (5.18)–(5.20) пригодны для случая аналитического задания исходной функции. Если функция задана в виде таблицы, то возникает задача приближенного отыскания коэффициентов Фурье по конечному числу имеющихся значений функции.
Таким образом, формулируется следующая задача практического, гармонического анализа: аппроксимировать на интервале (0, T) тригонометрический полином N- го порядка функцию у=f(х) , для которой известны m ее значений у k =f(х k ) при х k =kТ/m, где k= 0, 1, 2, …, m -1.
Тригонометрический полином для функции, определенной на интервале (0, Т), имеет вид:
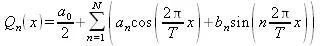 (5.21)
(5.21)
Коэффициенты а nи b nопределяются следующими соотношениями:
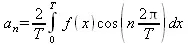 (5.22)
(5.22)
Читать дальше
Конец ознакомительного отрывка
Купить книгу

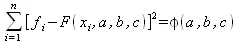 (5.14)
(5.14)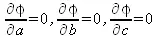
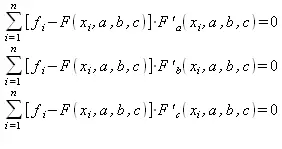 (5.15)
(5.15)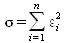 (5.16)
(5.16)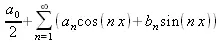 (5.17)
(5.17)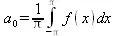 (5.18)
(5.18)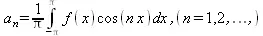 (5.19)
(5.19)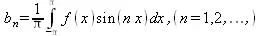 (5.20)
(5.20)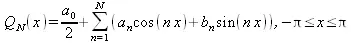
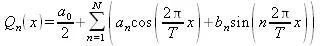 (5.21)
(5.21)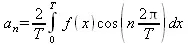 (5.22)
(5.22)










