Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

Как назначить частоты приемлемым способом? Можно ли найти решение, которое использует всего три цвета? Или два? Определение минимально возможного количества цветов на самом деле является NP-полной задачей — для этого подходят только экспоненциальные алгоритмы.

Мы не покажем алгоритм для решения данной задачи. Используйте то, чему вы научились к настоящему моменту, и попробуйте решить задачу самостоятельно. Это можно сделать на сайте UVA [54] Задача раскраски графа на сайте онлайновых экспертов UVA: https://code.energy/uva-graph-coloring . с онлайн-экспертом, который протестирует предложенное вами решение, выполнит ваш программный код и сообщит, работоспособен ли он. Если с кодом окажется все в порядке, эксперт также оценит время выполнения вашего кода в сравнении с тем, что написали другие люди. Дерзайте! Продумайте алгоритмы и стратегии решения данной задачи и испытайте их. Чтение книги может лишь подвести вас к решению. Взаимодействие с онлайновым экспертом даст вам практический опыт, необходимый для того, чтобы стать отличным программистом.

Поиск кратчайшего пути между узлами является самой известной графовой задачей. Системы навигации GPS проводят поиск в графе улиц и перекрестков для вычисления маршрута. Некоторые из них даже используют данные дорожного движения с целью увеличения веса ребер, представляющих улицы, где образовался затор.

Для поиска кратчайшего пути вполне можно использовать стратегии BFS и DFS, но это плохая идея. Одним из хорошо известных и очень эффективных способов поиска кратчайшего пути является алгоритм Дейкстры . В отличие от BFS, для запоминания просматриваемых вершин алгоритм Дейкстры использует очередь с приоритетом. Когда исследуются новые вершины, их связи добавляются в эту очередь. Приоритетом вершины является вес ребер, которые приводят ее в стартовую вершину. Благодаря этому следующая исследуемая вершина всегда оказывается самой близкой к месту, откуда мы начали.

Известны случаи, когда алгоритм Дейкстры зацикливается, не в силах найти конечную вершину. Процесс поиска может быть обманут отрицательным циклом , который приводит к бесконечному исследованию вершин. Отрицательный цикл — это путь в графе, чье начало и конец приходятся на одну вершину с весом ребер на пути, в сумме дающим отрицательное значение. Если вы ищете кратчайший путь в графе, где ребра могут иметь отрицательный вес, будьте начеку.

А что, если граф, в котором вы ищете, огромен? Для ускорения можно использовать двунаправленный поиск . Два процесса поиска выполняются одновременно: один начинает со стартовой вершины, другой — с конечной. Когда оказывается, что вершина, обнаруженная в одном пространстве поиска, также присутствует в другом, это значит, что у нас есть путь. Пространство поиска в таком случае вдвое меньше, чем в однонаправленным поиске. Посмотрите на рис. 5.4: серое пространство меньше белой области.

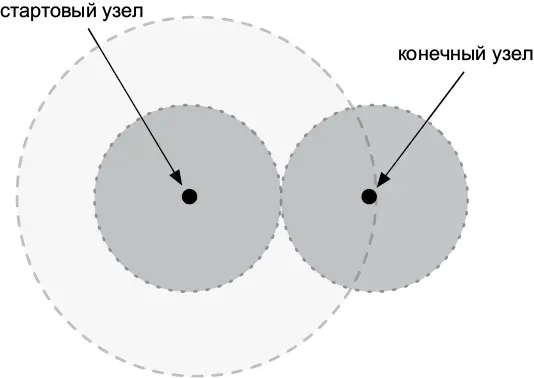
Рис. 5.4.Пространства однонаправленного и двунаправленного поиска

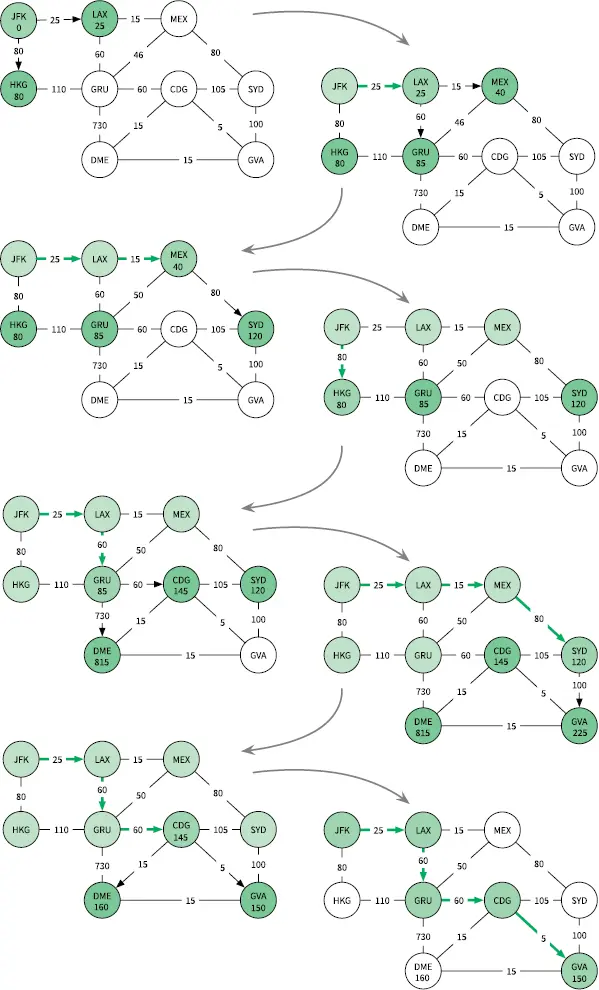
Рис. 5.5.Поиск кратчайшего маршрута от аэропорта JFK до аэропорта GVA при помощи алгоритма Дейкстры

Вы когда-нибудь задавались вопросом, как поисковой системе Google удается анализировать миллиарды веб-страниц и показывать вам самые подходящие? В этом процессе задействовано множество алгоритмов, но самым важным является алгоритм PageRank.

Прежде чем основать компанию Google, Сергей Брин и Ларри Пейдж работали научными сотрудниками в области computer science в Стэнфордском университете и занимались исследованием графовых алгоритмов. Они смоделировали Всемирную паутину в виде графа: веб-страницы — это вершины, и связи между ними — ребра.

Они решили, что если веб-страница получает много связей от других важных страниц, то она тоже должна быть важной. Опираясь на эту идею, они создали алгоритм PageRank. Он выполняется в несколько заходов. Вначале каждая веб-страница в графе имеет то же количество единиц значимости, что и остальные. После каждого захода она распределяет свои единицы среди страниц, ссылки на которые на ней размещены. Этот процесс повторяется до тех пор, пока все значения не стабилизируются. Стабилизированная оценка каждой страницы называется ее рангом, отсюда и название — PageRank (англ. «ранг страницы»). Используя этот алгоритм для определения важности веб-страниц, поисковая система Google быстро заняла доминирующую позицию среди других аналогичных сервисов.