Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

function insertion_sort(list)

····for i ← 2 … list.length

········j ← i

········while j and list[j-1] > list[j]

············list.swap_items(j, j-1)

············j ← j — 1

Выполните этот алгоритм на бумаге, с использованием большей частью отсортированного списка чисел. Для массивов, где не упорядочено незначительное число элементов, insertion_sort имеет сложность O ( n ). В этом случае он выполняет меньше операций, чем какой-либо другой алгоритм сортировки.

В отношении крупных наборов данных, о которых нельзя сказать, что они отсортированы большей частью, алгоритмы с временной сложностью O ( n 2) оказываются слишком медленными (см. табл. 3.2). Здесь нам нужны более эффективные подходы. Самыми известными высокоскоростными алгоритмами сортировки являются сортировка слиянием (см. раздел «Разделяй и властвуй» главы 3) и так называемая быстрая сортировка , оба имеют сложность O ( n log n ). Вот как алгоритм быстрой сортировки раскладывает по порядку колоду карт.

1. Если в колоде менее четырех карт, то упорядочить их — и работа завершена. В противном случае перейти к шагу 2.

2. Вынуть из колоды наугад любую карту, которая становится опорной .

3. Карты со значением больше , чем у опорной, кладутся в новую колоду справа ; карты с меньшим значением кладутся в новую колоду слева .

4. Проделать эту процедуру для каждой из двух только что созданных колод.

5. Объединить левую колоду, опорную карту и правую колоду, чтобы получить отсортированную колоду (рис. 5.1).

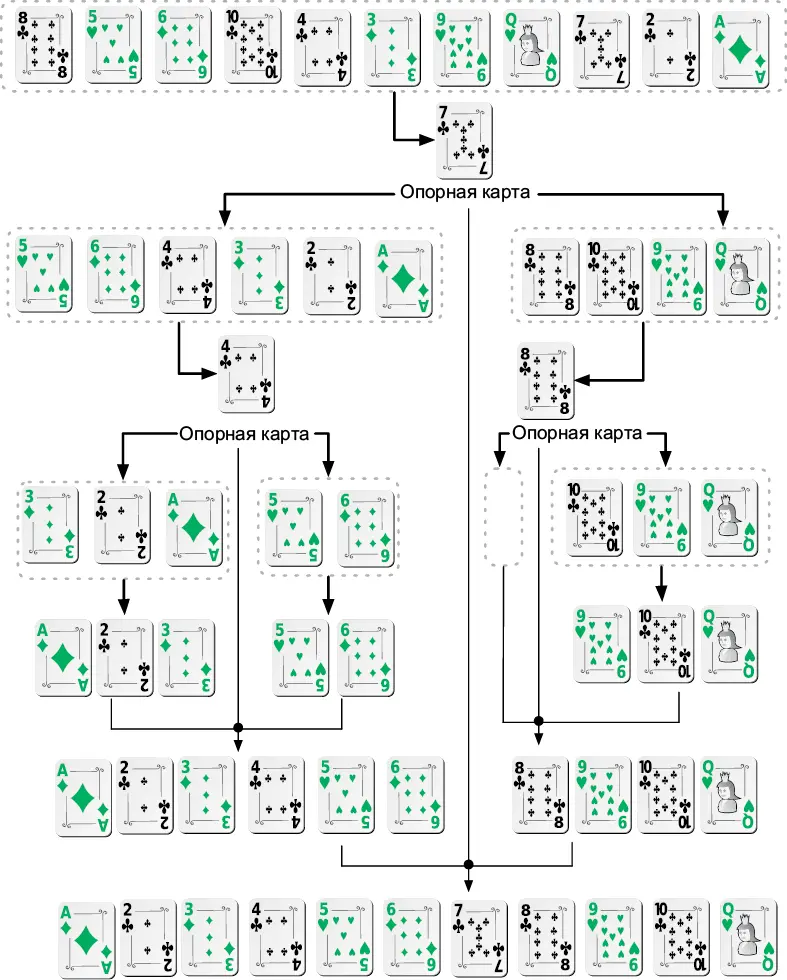
Рис. 5.1.Пример выполнения быстрой сортировки

Перетасуйте колоду карт и проделайте описанные шаги. Это поможет вам опробовать на практике алгоритм быстрой сортировки, а заодно укрепит ваше понимание рекурсии.

Теперь вы готовы решать большинство задач, связанных с сортировкой. Здесь мы осветили не все алгоритмы сортировки, так что просто помните, что их гораздо больше и каждый из них соответствует конкретным задачам.

Поиск определенной информации в памяти является ключевой операцией в вычислениях. Программисту очень важно владеть алгоритмами поиска. Самый простой из них — последовательный поиск : вы просматриваете все элементы один за другим, пока не будет найден нужный; как вариант, вы можете проверить все элементы, чтобы понять, что искомого среди них нет.

Легко заметить, что последовательный поиск имеет сложность O ( n ), где n — это общее количество элементов в пространстве поиска. Но на случай, когда элементы хорошо структурированы, есть более эффективные алгоритмы. В разделе «Структуры» предыдущей главы мы убедились, что извлечение данных, представленных в формате сбалансированного двоичного дерева поиска, стоит всего O (log n ).

Если ваши элементы хранятся в сортированном массиве, то их можно отыскать за такое же время, O (log n ), посредством двоичного поиска . Этот алгоритм на каждом шаге отбрасывает половину пространства поиска:

function binary_search(items, key)

····if not items

········return NULL

····i ← items.length / 2

····if key = items[i]

········return items[i]

····if key > items[i]

········sliced ← items.slice(i+1, items.length)

····else

········sliced ← items.slice(0, i-1)

····return binary_search(sliced, key)

На каждом шаге алгоритм binary_search выполняет постоянное число операций и отбрасывает половину входных данных. Это означает, что для n элементов пространство поиска сведется к нулю за log 2 n шагов. Поскольку на каждом шаге выполняется постоянное количество операций, алгоритм имеет сложность O (log n ). Вы можете выполнять поиск среди миллиона или триллиона элементов, и этот алгоритм по-прежнему будет показывать хорошую производительность.

Впрочем, существуют еще более эффективные алгоритмы. Если элементы хранятся в хеш-таблице (см. раздел «Структуры» предыдущей главы), достаточно вычислить хеш-ключ искомого элемента. Этот хеш даст его адрес! Время, необходимое для нахождения элемента , не меняется с увеличением пространства поиска. Не имеет значения, ищете вы среди миллионов, миллиардов или триллионов элементов, — количество операций останется постоянным, а значит, процесс имеет временную сложность O (1), он действует почти мгновенно.