Pedro Domingos - The Master Algorithm - How the Quest for the Ultimate Learning Machine Will Remake Our World

David Hume was the greatest of the empiricists and the greatest English-speaking philosopher of all time. Thinkers like Adam Smith and Charles Darwin count him among their key influences. You could also say he’s the patron saint of the symbolists. He was born in Scotland in 1711 and spent most of his life in eighteenth-century Edinburgh, a prosperous city full of intellectual ferment. A man of genial disposition, he was nevertheless an exacting skeptic who spent much of his time debunking the myths of his age. He also took the empiricist train of thought that Locke had started to its logical conclusion and asked a question that has since hung like a sword of Damocles over all knowledge, from the most trivial to the most advanced: How can we ever be justified in generalizing from what we’ve seen to what we haven’t? Every learning algorithm is, in a sense, an attempt to answer this question.

Hume’s question is also the departure point for our journey. We’ll start by illustrating it with an example from daily life and meeting its modern embodiment in the famous “no free lunch” theorem. Then we’ll see the symbolists’ answer to Hume. This leads us to the most important problem in machine learning: overfitting, or hallucinating patterns that aren’t really there. We’ll see how the symbolists solve it, and how machine learning is at heart a kind of alchemy, transmuting data into knowledge with the aid of a philosopher’s stone. For the symbolists, the philosopher’s stone is knowledge itself. In the next four chapters we’ll study the solutions of the other tribes’ alchemists.

To date or not to date?

You have a friend you really like, and you want to ask her out on a date. You have a hard time dealing with rejection, though, and you’re only going to ask her if you’re pretty sure she’ll say yes. It’s Friday evening, and there you sit with cell phone in hand, trying to decide whether or not to call her. You remember that the previous time you asked her, she said no. But why? Two times before that she said yes, and the one before those she said no. Maybe there are days she doesn’t like to go out? Or maybe she likes clubbing but not dinner dates? Being of an unusually systematic nature, you put down the phone and jot down what you can remember about those previous occasions:

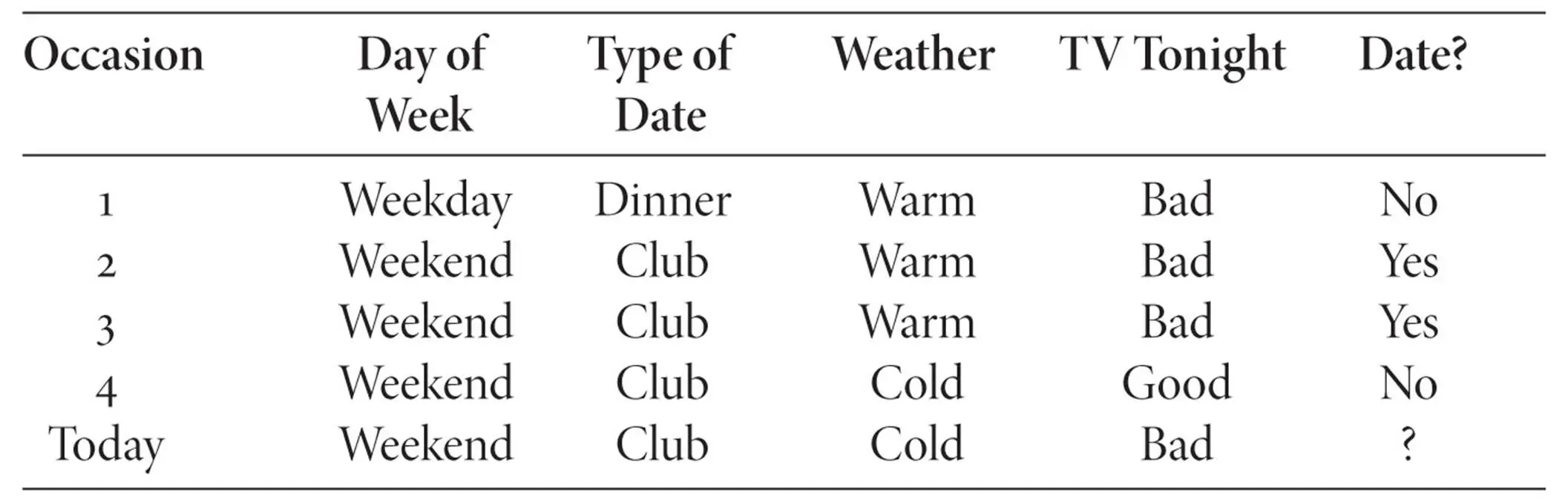
So… what shall it be? Date or no date? Is there a pattern that distinguishes the yeses from the nos? And, most important, what does that pattern say about today?

Clearly, there’s no single factor that correctly predicts the answer: on some weekends she likes to go out, and on some she doesn’t; sometimes she likes to go clubbing, and sometimes she doesn’t, and so on. What about a combination of factors? Maybe she likes to go clubbing on weekends? No, occasion number 4 crosses that one out. Or maybe she only likes to go out on warm weekend nights? Bingo! That works! In which case, looking at the frosty weather outside, tonight doesn’t look promising. But wait! What if she likes to go clubbing when there’s nothing good on TV? That also works, and that means today is a yes! Quick, call her before it gets too late. But wait a second. How do you know this is the right pattern? You’ve found two that agree with your previous experience, but they make opposite predictions. Come to think of it, what if she only goes clubbing when the weather is nice? Or she goes out on weekends when there’s nothing to watch on TV? Or-

At this point you crumple your notes in frustration and fling them into the wastebasket. There’s no way to know! What can you do? The ghost of Hume nods sadly over your shoulder. You have no basis to pick one generalization over another. Yes and no are equally legitimate answers to the question “What will she say?” And the clock is ticking. Bitterly, you fish out a quarter from your pocket and prepare to flip it.

You’re not the only one in dire straits-so are we. We’ve only just set out on our road to the Master Algorithm and already we seem to have run into an insurmountable obstacle. Is there any way to learn something from the past that we can be confident will apply in the future? And if there isn’t, isn’t machine learning a hopeless enterprise? For that matter, isn’t all of science, even all of human knowledge, on rather shaky ground?

It’s not like big data would solve the problem. You could be super-Casanova and have dated millions of women thousands of times each, but your master database still wouldn’t answer the question of what this woman is going to say this time. Even if today is exactly like some previous occasion when she said yes-same day of week, same type of date, same weather, and same shows on TV-that still doesn’t mean that this time she will say yes. For all you know, her answer is determined by some factor that you didn’t think of or don’t have access to. Or maybe there’s no rhyme or reason to her answers: they’re random, and you’re just spinning your wheels trying to find a pattern in them.

Philosophers have debated Hume’s problem of induction ever since he posed it, but no one has come up with a satisfactory answer. Bertrand Russell liked to illustrate the problem with the story of the inductivist turkey. On his first morning at the farm, the turkey was fed at 9:00 a.m., but being a good inductivist, he didn’t jump to conclusions. He first collected many observations on many different days under many different circumstances. Having been fed consistently at 9:00 a.m. for many consecutive days, he finally concluded that yes, he would always be fed at 9:00 a.m. Then came the morning of Christmas eve, and his throat was cut.

It would be nice if Hume’s problem was just a cute philosophical conundrum we could ignore, but we can’t. For example, Google’s business is based on guessing which web pages you’re looking for when you type some keywords into the search box. Their key asset is massive logs of search queries people have entered in the past and the links they clicked on in the corresponding results pages. But what do you do if someone types in a combination of keywords that’s not in the log? And even if it is, how can you be confident that the current user wants the same pages as the previous ones?

How about we just assume that the future will be like the past? This is certainly a risky assumption. (It didn’t work for the inductivist turkey.) On the other hand, without it all knowledge is impossible, and so is life. We’d rather stay alive, even if precariously. Unfortunately, even with that assumption we’re not out of the woods. It takes care of the “trivial” cases: If I’m a doctor and patient B has exactly the same symptoms as patient A, I assume that the diagnosis is the same. But if patient B’s symptoms don’t exactly match anyone else’s, I’m still in the dark. This is the machine-learning problem: generalizing to cases that we haven’t seen before .

But perhaps that’s not such a big deal? With enough data, won’t most cases be in the “trivial” category? No. We saw in the previous chapter why memorization won’t work as a universal learner, but now we can make it more quantitative. Suppose you have a database with a trillion records, each with a thousand Boolean fields (i.e., each field is the answer to a yes/no question). That’s pretty big. What fraction of the possible cases have you seen? (Take a guess before you read on.) Well, the number of possible answers is two for each question, so for two questions it’s two times two (yes-yes, yes-no, no-yes, and no-no), for three questions it’s two cubed (2 × 2 × 2 = 2 3), and for a thousand questions it’s two raised to the power of a thousand (2 1000). The trillion records in your database are one-gazillionth of 1 percent of 2 1000, where “gazillionth” means “zero point 286 zeros followed by 1.” Bottom line: no matter how much data you have-tera- or peta- or exa- or zetta- or yottabytes-you’ve basically seen nothing . The chances that the new case you need to make a decision on is already in the database are so vanishingly small that, without generalization, you won’t even get off the ground.