Валентин Арьков - Применение гистограмм в управлении качеством

Вопрос. Когда возникает асимметрия распределения?

Для моделирования асимметричного распределения используем бета-распределение со следующими параметрами:

Alpha = 2

Beta = 5.

Это стандартное асимметричное распределение, хорошо изученное в теории вероятностей. Его используют, в частности, для оценки длительности работ при управлении проектами. Название указывает на то, что в расчётах используется специальная математическая Бета-функция. Сейчас мы не углубляемся в математические дебри. В данной работе нас будет интересовать только форма графика и возможности имитационного моделирования.

Познакомимся с формой бета-распределения. Используем следующую функцию:

BETA. DIST (x, alpha, beta, cumulative).

Создаём столбец значений от 0 до 1 с шагом 0,01.

Находим значения функции плотности вероятности (probability density function, PDF):

BETA. DIST (x, 2, 5, 0).

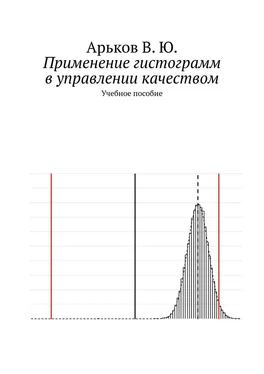
Строим график функции (рис. 9.3.1). График начинается в точке х = 0. Можно видеть явное нарушение симметрии.

Рис. 9.3.1. Бета-распределение

Задание. Постройте график бета-распределения.

В теории вероятностей уже определили теоретическое среднее для такого распределения. Формула среднего для бета-распределения приводится на рис. 9.3.2.

Рис. 9.3.2. Среднее для бета-распределения

Задание. Вычислите значение среднего с точностью до пяти знаков после запятой.

Сформируем график желаемого распределения (рис. 9.3.3). Нам нужно преобразовать случайную величину со стандартным бета-распределением в то, что показано на зарисовке. Нам придётся сделать пересчёт координат в порядковые номера — чтобы нанести кривую распределения на комбинированную диаграмму..

Рис. 9.3.3. Зарисовка распределения

Задание. Сделайте зарисовку для пересчёта координат.

Разберёмся, как нам предстоит проводит пересчёт координат. Для номинального размера 1000 ммслучайная величина b(аргумент бета-распределения) должна быть равна среднему значению, то есть 0,29. Для размера 1020 ммаргумент равен 1. Строим пропорцию и получаем значение «икса» при b = 0 (рис. 9.3.4).

Рис. 9.3.4. Оценка параметров распределения

Нам нужно расположить случайную величину в поле допуска, как показано на зарисовке рис. 9.3.3. Для этого мы сгенерируем случайную величину b, а затем преобразуем её следующим образом:

x = 992 +28 b.

Как мы получили эту формулу? Мы определили, что начало кривой b = 0 будет в точке х = 992. Это смещение по оси «икс». В формуле пересчёта это свободный член уравнения.

Случайная величина bменяется от 0 до 1. При этом размер детали, то есть величина х, меняется от 992 до 1020. Это в 28 раз больше. Получаем масштабный коэффициент 28.

Задание. Составьте формулу для преобразования случайной величины.

Переходим к имитационному моделированию. Будем использовать метод ФУНКЦИОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ. Чтобы сгенерировать случайные числа с заданным распределением, вначале генерируют равномерное распределение, а потом к нему применяют обратную функцию заданного распределения (рис. 9.3.5). Здесь F (x) — интегральная функция заданного распределения, p (x) — функция плотности вероятности. Пока что выглядит довольно сложно. Как это работает — мы постепенно разберём.

Рис. 9.3.5. Метод преобразования

Вопрос. Какие два этапа включает моделирование произвольного распределения?

Итак, нас ожидает первый этап моделирования — равномерное распределение. С помощью генератора случайных чисел мы создаём столбец случайных чисел с РАВНОМЕРНЫМ РАСПРЕДЕЛЕНИЕМ на интервале [0, 1](рис. 9.3.6). Напомним, что в каждом упражнении задаём новое начальное состояние генератора Random Seed. Полученные случайные числа размещаем в колонке Uniform(равномерное распределение).

Рис. 9.3.6. Генератор равномерного распределения

Задание. Сгенерируйте числа с равномерным распределением.

Теперь второй этап моделирования — обратная функция. Мы пропускаем полученную случайную величину с равномерным распределением через обратную функцию распределения и получаем заданное распределение. Для такого преобразования мы будем использовать встроенную функцию Excel — обратную интегральную функцию бета-распределения (inverted beta distribution):

BETA.INV (probability, alpha, beta).

Аргументы функции — вероятность и параметры распределения. На выходе функции получаем случайную величину с бета-распределением (рис. 9.3.7).