Валентин Арьков - Корреляционный и регрессионный анализ в Excel

© Валентин Юльевич Арьков, 2019

ISBN 978-5-0050-4576-8

Создано в интеллектуальной издательской системе Ridero

Данная лабораторная работа позволяет освоить базовые методы исследования взаимосвязей в электронной таблице — корреляционный и регрессионный анализ.

При выполнении лабораторной работы используются знания и навыки, полученные на предыдущих занятиях.

Условные обозначения:

— жирный шрифт — названия функций и пунктов меню;

— КНОПКИ на экране компьютера;

— КЛАВИШИ на клавиатуре компьютера.

Описывается работа в англоязычной версии Microsoft Excel из пакета Office 365. В тексте приводятся названия пунктов меню и функций на английском и на русском языках. На рисунках используется английская версия пакета.

В данной лабораторной работе рассматривается корреляционная зависимость, или корреляция [1—4].

В работе для изучения взаимосвязи используются методы корреляционного и регрессионного анализа, а также сводка и группировка данных. Работа выполняется в пакете Excel [5].

Корреляционный анализ позволяет оценить степень тесноты связи. Регрессионный анализ используется для построения линейных и нелинейных моделей.

На первом этапе исходные данные получают путём имитационного моделирования. На втором этапе проводится анализ реальных данных.

Требования к оформлению отчёта приведены в описании предыдущей лабораторной работы [6].

Корреляция — это связь между двумя случайными величинами, которые часто называют следующим образом:

X — факторный признак;

Y — результативный признак.

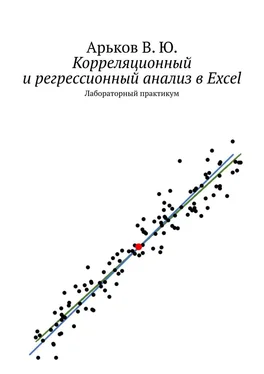
Изображение исходных данных называется диаграммой разброса. Каждая пара чисел Xи Yизображается отдельной точкой. Точки между собой не соединяют.

Пример диаграммы разброса для корреляционной зависимости показан на рисунке ниже.

Корреляция

Варианты заданий представлены в таблицах.

В каждом варианте рассматриваются два набора данных — примеры линейной и нелинейной регрессии. Анализ проводится для обоих случаев.

Факторный признак Х — случайная величина с равномерным распределением.

Случайная составляющая Е — случайная величина со стандартным нормальным распределением (нулевое среднее и единичная дисперсия).

Результативный признак Yвычисляется по формуле.

Объём выборки n = 200.

На новом листе опишите вариант задания.

Сделайте зарисовки общей формы зависимости и диаграммы разброса на бумаге. Вставьте зарисовку в отчёт.

Для построения линейной функции оцените значения на границах диапазона значений факторного признака. Оцените случайный разброс по правилу трёх сигм.

Зарисовка линейной функции

Для зарисовки графика параболы дополнительно определите координаты её вершины кривой и направление ветвей.

Выберите масштаб так, чтобы данные занимали всё поле графика. Метки на осях должны быть круглыми числами.

Зарисовка нелинейной функции

Сгенерируйте исходные данные в соответствии c вариантом задания.

Вызовите надстройку:

Data Analysis

Анализ данных.

Используйте функцию:

Random Number Generation

Генерация случайных чисел.

Округлите сгенерированные числа до целых.

Задавайте разные начальные состояния генератора для получения фактора Хи случайной составляющей Е.

Для округления используйте функцию

ROUND (number, num_digits)

ОКРУГЛ (число; число разрядов).

Для округления до целых укажите нулевое число разрядов после запятой.

В отчёте опишите параметры генератора случайных чисел.

В дальнейшей работе используйте округлённые значения Хи Y.

Постройте диаграмму разброса:

Insert — Charts — Insert Scatter (X, Y) or Bubble Chart — Scatter — Scatter

Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму — Точечная — Точечная.

Настройте оформление графика. Задайте масштаб и информативные заголовки. Пример оформления показан на рисунке.

Оформление графика

В отчёте опишите внешний вид графиков.