Валентин Арьков - Применение гистограмм в управлении качеством

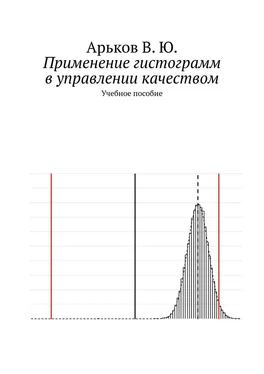
На рис. 9.1.1. приводятся примеры несимметричного распределения (слева) и симметричного (справа). МОДА — это положение максимума, пика кривой. Это значение случайной величины, которое встречается чаще всего. Это значение с максимальной вероятностью. Среднее совпадает с модой для нормального распределения, а также для любого симметричного распределения.

Вопрос. Что такое мода?

Вопрос. Как расположены среднее и мода на графике нормального распределения?

Моду можно определить по виду графика, а среднее значение нужно вычислять. Поэтому при анализе гистограммы на график нужно дополнительно наносить среднее значение, вычисленное по выборке.

Рис. 9.1.1. Мода и среднее

Вопрос. Почему среднее приходится наносить на график?

Среднее значение вычисляют по выборке с помощью формулы средней арифметической простой (рис. 9.1.2). Другое название этой характеристики — ВЫБОРОЧНОЕ СРЕДНЕЕ.

Рис. 9.1.2. Выборочное среднее

Вопрос. По какой формуле вычисляют среднее?

Когда среднее значение начинает «уходить», отклоняться от номинального размера, — это ещё не брак. Но такое изменение — это сигнал о начале нежелательных изменений. Если среднее продолжит «дрейфовать», часть продукции может выйти за границу поля допуска. А это уже брак.

Вопрос. Почему нужно следить за средним значением?

Смоделируем ситуацию, когда среднее существенно «ушло» от номинального значения и часть изделий уже оказалась за границей допуска. Будем моделировать случайную величину, у которой среднее плюс две сигмы соответствует верхней границе допуска (рис. 9.1.3). Это означает, что 2,5% изделий окажется за границей допуска и будет забраковано. В данном случае мы рассматриваем правый «хвост» распределения (рис. 9.1.4).

Рис. 9.1.3. Оценка среднего

Рис. 9.1.4. Хвосты распределения

Для нулевого варианта задания имеем:

Среднее = ВГД — 2 сигмы = 1040 — 2 x 5 = 1030.

Далее мы будем моделировать случайную величину с этими параметрами:

Задание. Оцените среднее и сделайте зарисовку формы распределения на поле допуска.

Проведём анализ гистограммы, как описано в предыдущих разделах:

— С помощью надстройки моделируем случайную величину со средним 1030 мм и сигмой 5 мм. Задаём новое начальное состояние генератора случайных чисел (рис. 9.1.5).

— Вычисляем выборочное среднее.

— Проводим группировку данным.

— Строим гистограмму.

— Строим кривую нормального распределения с параметрами выборки.

— Наносим границы допуска и номинал, а также выборочное среднее.

— Изучаем и описываем гистограмму.

Рис. 9.1.5. Генератор

Для всех линий на графике строим вспомогательные таблички (рис. 9.1.6).

Рис. 9.1.6. Вспомогательные таблички

Задание. Постройте вспомогательные таблички.

Строим график, наносим все линии и делаем необходимые настройки. Получаем окончательное оформление гистограммы (рис. 9.1.7).

Рис. 9.1.7. Оформление гистограммы

На графике видно, какая часть гистограммы выходит за верхнюю границу допуска, — как мы и планировали. Можно увидеть отклонение среднего от номинала. Форма гистограммы соответствует нормальному распределению.

Задание. Постройте и оформите гистограмму.

Сигма (среднее квадратичное отклонение) — вторая по важности характеристика распределения. Этот параметр определяет разброс вокруг среднего значения. Если ухудшаются свойства или настройки оборудования, может увеличиваться технологический разброс. Тогда хвосты распределения могут выйти за границы допуска — даже при поддержании среднего в районе номинала.

Смоделируем следующую ситуацию (рис. 9.2.1):

Среднее = Номинал

НГД = Среднее — 2 Сигмы

ВГД = Среднее +2 Сигмы

Рис. 9.2.1. Увеличенная сигма

В нулевом варианте получаем:

Сигма = 20 мм.

Задание. Определите сигму и сделайте зарисовку распределения на поле допуска с указание размеров.

Скопируем предыдущую страницу электронной таблицы и вставим её в конец рабочей книги:

Move or Copy — Create a Copy — (move to end).

Это наш шаблон для вычислений и построения графика.

Окончательный вид гистограммы приводится на рис. 9.2.2.

Рис. 9.2.2. Оформление гистограммы

Задание. Сгенерируйте данные и постройте гистограмму.

Нарушение симметрии распределения может происходить по разным причинам. Например, возможны ситуации, когда есть физический предел для минимального значения, а максимальное значение не ограничено. Такими показателями могут быть количество жалоб, аварий или отказов. Их минимальное количество равно нулю, а отрицательные значения невозможны. При этом распределение будет скошено влево. Естественно, при анализе гистограммы необходимо учитывать физическую природу производственного процесса и понимать, есть ли предпосылки к асимметрии. Если нарушение симметрии не обусловлено естественными причинами, потребуется провести исследование — особенно если за некоторое время до этого распределение было близко к нормальному.