Никита Сергеев - Аналитика и Data Science. Для не-аналитиков и даже 100% гуманитариев…

Именно наличие значимыхзакономерностей позволяет распространять полученные на выборке результаты на всю генеральную совокупность.

Как это работает? Например, мы хотим выяснить, проводят ли женщины больше времени в соцсетях, чем мужчины. Мы взяли определенную выборку из 1000 женщин и мужчин и обнаружили, что мужчины в среднем проводят в сетях 5 часов в неделю, а женщины 7 часов. Получается, что женщины на 2 часа (на 40%!) больше сидят в сетях.

Но можем ли мы на этих результатах утверждать, что в принципе все другие женщины больше сидят в соцсетях, чем мужчины? Возможно, мы получили различие случайно, и оно характеризует только эту выборку, а не всю генеральную совокупность…

И вот тут мы сначала определяем вероятность для H 0: что разницы по «просиживанию» в соцсети между мужчинами и женщинами нет. Или, другими словами, рассчитываем вероятность ошибки насчет того, что женщины сидят в соцсети больше мужчин.

И если вероятность ошибиться будет менее 5%, то мы можем говорить о том, что обнаружили статистически значимое различие – и таки можем говорить, что все женщины проводят в сети больше времени.

Почему берется такое низкое значение вероятности ошибки? Скажу, что на самом деле часто используют даже ниже 1% или менее. От чего зависит? На самом деле от отрасли и сложившейся в ней практики. Например, в медицине цена ошибки может быть высокой и там значения вероятности ошибок принимают обычно очень низкими.

В целом, общепринятая интерпретация вероятности ошибки (или значимости результатов) в среде аналитиков следующая ( рис. 15 ):

Рис. 15. Уровни значимости и их интерпретация

Прочитав этот раздел, я думаю, Вы уже поняли, насколько нами могут манипулировать с помощью различных опросов и исследований, в которых утверждается, что «женщины / мужчины лучше руководят», «опрошенные считают честным кандидата в президенты», «у ряда пациентов наблюдалось улучшается самочувствие после применения препарата» и т. д.

Широкой публике просто часто выдают информацию без обозначения репрезентативности выборки, заложенной модели, еще и в придачу не указывая, являются ли эти взаимосвязи статистически значимыми.

Колоколообразную кривую знают и наслышаны все (она же колокол Гаусса, гауссовское распределение – рис. 16 ).

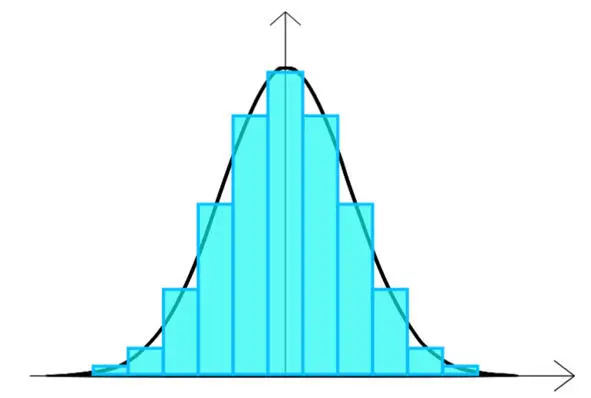
Рис. 16. То самое ОНО – нормальное распределение

Я о ней уже упоминал вначале, когда говорил об особенностях социально-экономической реальности в сравнении с естественно-технической.

И почему-то многие уверены, что этой кривой подчиняется все. На самом деле в реальности кривая нормального распределения чаще всего проявляется в физических параметрах, ограниченных физическими законами – гравитация, размеры, вес организмов определенного вида и т. д.

В социально-экономической реальности скорее наоборот – Вы будете встречать отсутствие нормального распределения. Оно буде скорее скошено вправо или влево, или очень сжато по оси ОХ или ОY ( рис. 17 ).

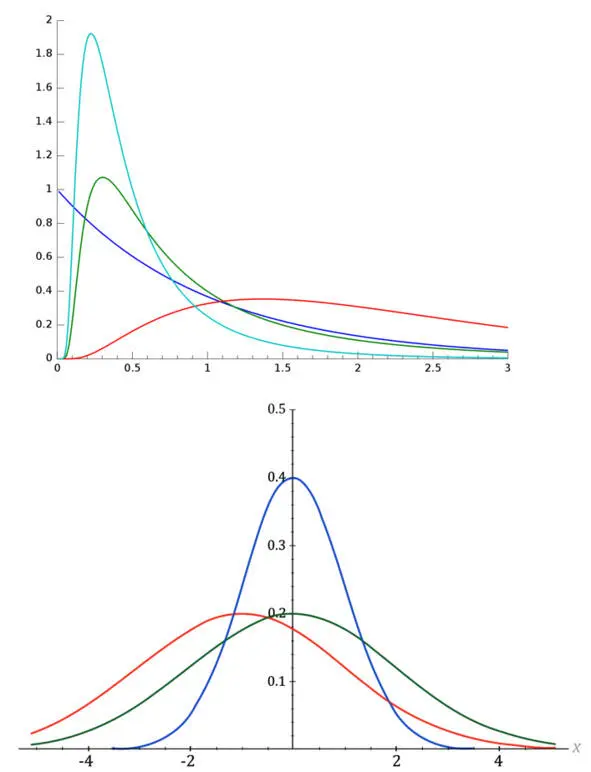
Рис. 17. Примеры реальных распределений в социально-экономической реальности

90% жителей страны владеют 2% капитала. 2 певца забирают 95% популярности. 99% тиража всех книг приходится на 1% авторов и т. д.

В любом случае на практике реальное распределение отклоняется от этой кривой. Да и выборки данных, строго соответствующие нормальному распределению, на практике, как правило, не встречаются.

Но тем не менее, в статистике перед исследованием важно понимать соответствует ли распределение наших данных по каждой переменной нормальному распределению.

Для переменных, которые нормально распределены – используются одни параметры и критерии для сравнения (и среднее значение, дисперсия, стандартное отклонение – в этом случае информативные показатели).

Для тех переменных, которые не соответствуют нормальному распределению – другие критерии (тут скорее более информативными будут ранги, мода, медиана и т.д.).