Владимир Брюков - Как предсказать курс доллара. Расчеты в Excel для снижения риска проигрыша

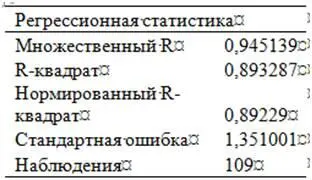
Параметры, представленные в таблице 2.2, оценивают уровень аппроксимации фактических данных, полученный с помощью данного уравнения регрессии. Так, здесь R2=0,8933, а это означает, что линейный тренд объясняет 89,33 % всей динамики курса доллара к рублю, то есть в данном случае мы получили довольно высокий уровень коэффициента детерминации.

Можно также сказать несколько иначе: в данном уравнении тренда изменения независимой переменной «Порядковый номер торгового дня» на 89,33 % объясняет динамику зависимой переменной «Курс доллара к рублю». Кстати, при графическом способе решения уравнения тренда – по тем же рыночным данным и за тот же период времени – величина коэффициента детерминации R2 также оказалась равна 0,8933 – см. рис. 1.20.

Чем ближе коэффициент детерминации к 1, тем теснее связь между переменными, включенными в уравнение регрессии. Как я уже говорил, для целей торговли, нужно использовать линейный тренд с коэффициентом детерминации не ниже R2=0,80.

Когда максимальное значение коэффициента детерминации равно 1, то в этом случае можно сказать, что динамика зависимой переменной на 100% объясняется изменением независимой переменной. В этом случае также говорят, что между переменными существует функциональная связь. Это будет означать, что в динамике тренда нет случайной компоненты, но, вполне очевидно, что на практике этого в колебаниях курсов валют никогда не бывает.

Нормированный R2 имеет смысл использовать, когда нам придется сравнивать уравнения регрессии с различным количеством включенных в него независимых переменных. Дело в том, что при добавлении в уравнении регрессии независимых переменных величина коэффициента детерминации R2 соответственно растет. Поэтому для того чтобы сделать сравнения коэффициентов детерминации между уравнениями регрессии с разным числом факторов сопоставимыми, используется нормированный (скорректированный) R2, величина которого корректируется в сторону уменьшения при добавлении в уравнение дополнительных факторов. При прочих равных условиях предпочтение будем отдавать тому уравнению, в котором нормированный R2 будет выше.

Еще один параметр в таблице 2.2. Наблюдения=109 говорит о том, что в данное уравнение регрессии получено на основе данных по итогам торгов за 109 торговых дней.

Таблица 2.2. Регрессионная статистика

Источник: расчеты автора

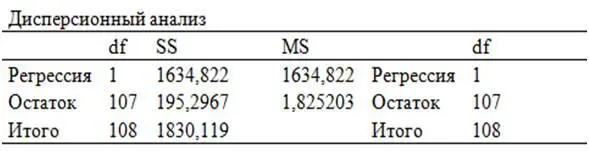
В таблице 2.3 дается дисперсионный анализ (от лат. dispersio, что в переводе означает разброс, рассеяние), суть которого заключается в изучении влияния одной или нескольких независимых переменных на зависимую результативную переменную. В данном случае дается анализ изменения результативного признака «Курс доллара к рублю» под воздействием включенной в уравнение регрессии одной независимой переменной – «Порядковый номер торгового дня». Здесь в столбце значимость F дается уровень статистической значимости в целом уравнения регрессии.

Следует иметь в виду, что чем ближе значимость F к нулю, тем более обоснованным будет наш вывод о статистической значимости в целом всего уравнения регрессии. Причем, если значимость F меньше 0,01, то можно говорить о статистической значимости уравнения регрессии с 1% значимостью (или 99% уровнем надежности). Если значимость F больше 0,01, но меньше 0,05, то тогда говорят о статистической значимости уравнения регрессии с 5% значимостью (или 95% уровнем надежности).

Таблица 2.3. Дисперсионный анализ

Источник: расчеты автора

Правда, значимость F-критерия в данном случае дается Excel в экспоненциальном виде, который может быть непонятен для некоторых неискушенных в математике читателей. Для тех, кто хочет разобраться, хочу заметить, что число в экспоненциальном виде легко преобразовать в обычную цифру. Например, 1,60E+04=1*10^4=16000, а 1,60E-04 = 1*(1/10^4)=0,00016. При этом E+04 в данном случае означает умножение 1,60 на 104, а E-04 означает умножение 1,60 на 10-4 или (что одно и то же) умножение 1,60 на 1/104.

Тот, кто не хочет ломать голову над числом в экспоненциальном виде, может эту проблему решить, преобразовав формат данной ячейки с экспоненциального в числовой. С этой целью наведем курсор мышки на эту ячейку, и, щелкнув ее правой кнопкой, в появившемся диалоговом окне выберем опцию ФОРМАТ ЯЧЕЕК. После этого появится диалоговое окно ФОРМАТ ЯЧЕЕК, в котором нужно выбрать опцию ЧИСЛОВОЙ – см. рис. 2.2. В результате нам удастся выяснить, что значимость F=0,00. Следовательно, в данном случае значимость F меньше 0,01, то есть можно сделать вывод, об 1% статистической значимости этого уравнения регрессии с (или 99% уровнем надежности). Хочу обратить внимание читателей, что для большей надежности для целей прогнозирования лучше использовать уравнения регрессии со значимостью F меньше 0,01.