Владимир Брюков - Как предсказать курс доллара. Расчеты в Excel для снижения риска проигрыша

Например, при наличии автокорреляции со сдвигом (лагом) в один период времени (в данном случае в один торговый день) величина остатка наблюдения 1 влияет на величину остатка наблюдения 2, а величина последнего ‑ на величину остатка в наблюдении 3 … И так далее.

Выявить автокорреляцию в остатках можно: либо с помощью критерия Дарбина-Уотсона (см. подробности – стр. 436-442, в Эконометрика: Учебник/И.И.Елисеевой, С.В. Курышева, Т.В. Костеева и др.; Под. ред. И.И.Елисеевой. ‑ 2-е изд., перераб. и доп. – М.; Финансы и статистика, 2006), либо построив точечный график остатков с определенным лагом (отставанием).

Критерия Дарбина-Уотсона нельзя применять для моделей авторегрессии, то есть для уравнений, в которых результативная переменная зависит от своей лаговой переменной. Кроме того графический способ выявления автокорреляции в остатках, на наш взгляд, более проще, поэтому остановимся на последнем. Поскольку мы планируем делать прогнозы с прогнозируемым горизонтом в один день (при большем горизонте точность их снижается), то, следовательно, нам нужно посмотреть – нет ли автокорреляции в остатках с лагом в один торговый день. С этой целью мы построим таблицу 2.7, в которой будет 108, а не 109 наблюдений, так как одно наблюдение мы потеряли после создания лаговой переменной.

Таблица 2.7. Тестирование на автокорреляцию в остатках однофакторного уравнения регрессии

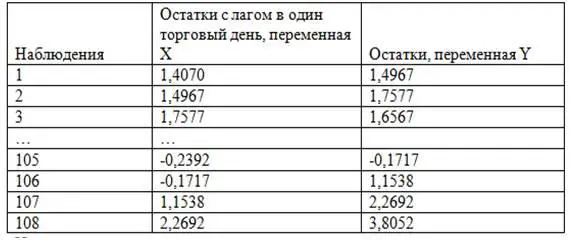
Источник: расчеты автора

На основе данных этой таблицы и используя алгоритм № 2 «Построение графика в Microsoft Excel» можно построить график зависимости «Остатков» от «Остатков с лагом в один торговый день». Правда, в шаге 2 алгоритма № 2 после выбора в панели инструментов кнопки Вставка (в Excel 2007 года), либо кнопки Мастер диаграмм (в Excel 1997-2003 года), нужно щелкнуть левой кнопкой мышки не опцию График (подходит к анализу зависимости результативной переменной от независимой переменной ‑ время), а опцию ТОЧЕЧНЫЙ (подходит к анализу зависимости результативной переменной от независимой переменной, не обозначающей время).

В результате получим следующий график зависимости «Остатков» от «Остатков с лагом в один торговый день»‑ см. рис.2.5. Судя по тому, что точки на графике растут слева направо, можно сделать вывод о наличии положительной автокорреляции в остатках.

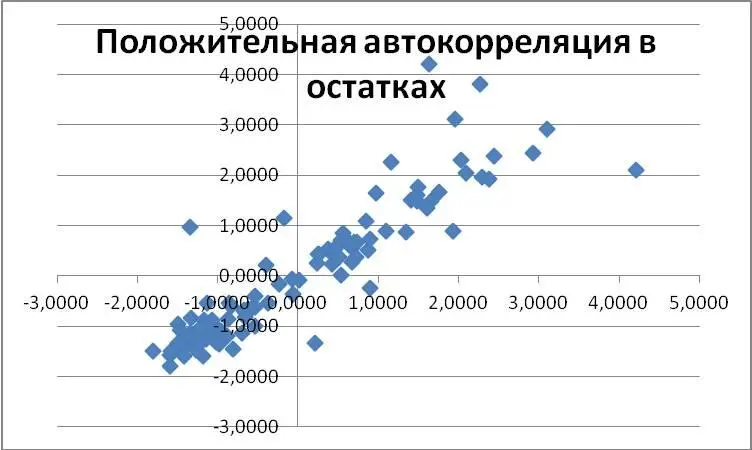
Рис. 2.5

В том случае, когда точки на графике снижаются слева направо, можно сделать вывод о наличии отрицательной автокорреляции в остатках – см. рис. 2.6.. Бывают и другие формы автокорреляционной зависимости, но на них мы не будем останавливаться.

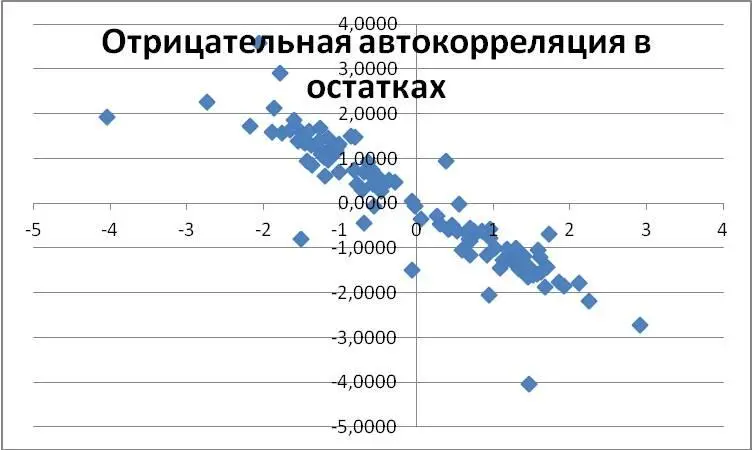
Рис. 2.6

Если же на графике остатков налицо круговой разброс точек в хаотичном порядке, то тогда можно сделать вывод об отсутствии автокорреляции или ее близости к нулю – см. рис. 2.7.

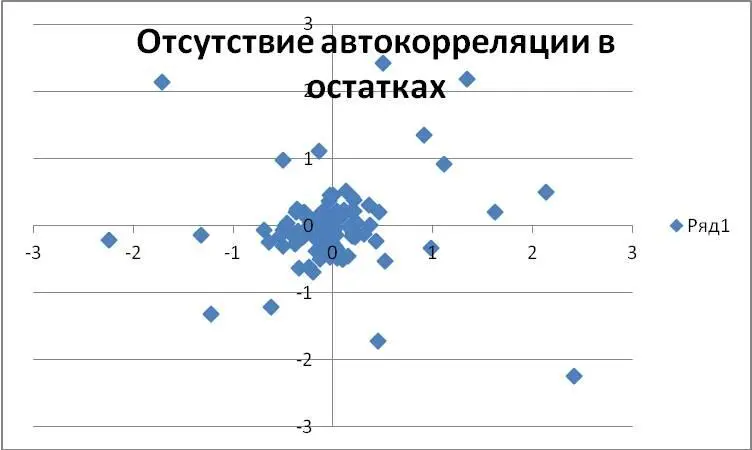
Рис. 2.7

Используя алгоритм № 6 «Как решить уравнение регрессии в Excel» можно решить уравнение регрессии с этими двумя переменными. При этом выяснится, что свободный член (исходный уровень) в этом уравнении регрессии окажется статистически незначимым.

Поэтому мы решим его без свободного члена, а затем, воспользовавшись алгоритмом № 4 «Построение графическим способом линейного тренда в Excel», получим следующий график с построенным по нему трендом ‑ см. рис.2.8. Исходя из полученного уравнения регрессии Y = 0,9398X, можно сделать вывод, что рост «Остатков с лагом в один день» на 1 рубль приводил к увеличению «Остатков» в среднем на 93,98 коп. При этом коэффициент детерминации R² = 0,8261 говорит о том, что динамика «Остатков» на 82,61% объясняется колебаниями «Остатков с лагом в один день».

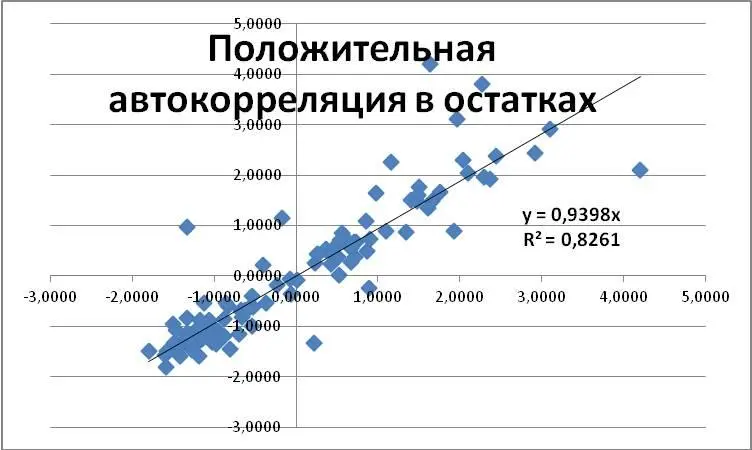
Рис. 2.8

Таким образом в главе 2 мы научились решать однофакторное уравнение регрессии, а также тестировать его статистическую значимость и значимость каждого из его членов. Вместе с тем в остатках, полученных после однофакторного уравнения регрессии, выявлена автокорреляция, что не дает нам возможность использовать его в прогнозах для биржевой торговли. О том, как можно устранить автокорреляцию, речь пойдет в главе 3.