Владимир Брюков - Как предсказать курс доллара. Расчеты в Excel для снижения риска проигрыша

Воспользуемся алгоритмом № 5. «Как решить уравнение регрессии в Excel» из главы 2, чтобы решить новое уравнение регрессии. Алгоритм действий будет аналогичным за исключением того, что в это уравнение регрессии будут включены две независимые переменные, о которых мы уже говорили – Xt и Xo, а также зависимая от них результативная переменная Y.

Однако прежде чем приступить к решению двухфакторного уравнения регрессии приведем краткий алгоритм оценки адекватности уравнения регрессии на основе вывода итогов, оценки средней ошибки аппроксимации и выявления автокорреляции в остатках. Этим мы уже занимались в главе 2, но в данном случае этот алгоритм представляет собой краткое резюме для проверки адекватности уравнений регрессии. Им читателю будет удобно пользоваться при оценке адекватности решенных им уравнений регрессии.

Алгоритм № 6 «Оценка адекватности уравнения регрессии».

Шаг 1. Принятие решения о статистической значимости уравнения регрессии.

1.1. Чем ближе R-квадрат или нормированный R-квадрат (если сравниваются уравнения регрессии с различным количеством включенных в него независимых переменных) к 1, тем лучше, что дает отличный критерий для выбора одного из нескольких уравнений регрессии.

1.2. Значимость F должна быть меньше 0,05 – при 5% уровне статистической значимости или 95% уровне надежности; должна быть меньше 0,01 ‑ при 1% уровне статистической значимости или 99% уровне надежности.

Шаг 2. Принятие решения о статистической значимости коэффициентов уравнения регрессии .

2.1. P-Значение должно быть меньше 0,05 – при 5% уровне статистической значимости или 95% уровне надежности; P-Значение должно быть меньше 0,01 ‑ при 1% уровне статистической значимости или 99% уровне надежности.

2.2. Коэффициенты регрессии и свободного члена при переходе от столбца Нижние и к столбцу Верхние (при заданном уровне надежности) не должны менять свой знак. Если смена знака происходит, то коэффициенты данного уравнения регрессии считаются статистически незначимыми.

Шаг 3. Принятие решения о возможности прогнозирования по данной статистической модели.

3.1. Средняя ошибка аппроксимации не должна быть выше 7-10%.

Шаг 4. Проверка автокорреляции в остатках.

4.1. Проверка графическим способом остатков, полученных после решения уравнения регрессии, на наличие в них автокорреляции. В случае обнаружения автокорреляции в остатках это уравнение регрессии не годится для прогнозирования. Для устранения автокорреляции в остатках существует ряд способов. Но мы для ее устранения будем решать двухфакторное уравнение регрессии, включив в него новую переменную ‑ «Остатки с лагом в один день».

Используем алгоритм № 6 «Оценка адекватности уравнения регрессии» для анализа информации, полученной после вывода итогов по двухфакторному уравнению регрессии. Судя по таблице 3.2, R2 в данном случае оказался равен 0,9808, Иначе говоря, это уравнение регрессии объясняет 98,08% всех колебаний зависимой (результативной) переменной «Курс доллара к рублю». При этом нормированный R2 равен 0,9805, то есть больше нормированного R2=0,8923, полученного после решения однофакторного уравнения. Следовательно, по этому критерию двухфакторному уравнению, безусловно, нужно отдать предпочтение.

Таблица 3.2. Регрессионная статистика

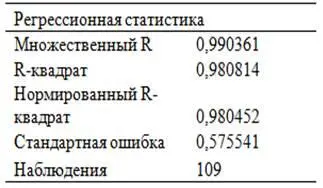
Источник: расчеты автора

В таблице 3.3 нас интересует Значимость F, которое первоначально Excel дает в экспоненциальном виде. Но с помощью опции ФОРМАТ ЯЧЕЕК мы преобразовали его в числовой вид и убедились, что Значимость F =0,00. Следовательно, в данном случае значимость F меньше 0,01, то есть можно сделать вывод, об 1% статистической значимости полученного нами двухфакторного уравнения регрессии (или 99% уровнем надежности).

Таблица 3.3. Дисперсионный анализ

Источник: расчеты автора

В таблице 3.4 надо обратить внимание на P-Значения коэффициентов уравнения регрессии, которые первоначально Excel дает в экспоненциальном виде. Но с помощью опции ФОРМАТ ЯЧЕЕК мы преобразовали их в числовой вид. При этом все три P-Значения равны 0,00. Следовательно, в данном случае P-Значения меньше 0,01, то есть можно сделать вывод, об 1% статистической значимости всех коэффициентов полученного нами двухфакторного уравнения регрессии (или 99% уровнем надежности). При этом все коэффициенты данного уравнения регрессии при переходе от столбца Нижние и к столбцу Верхние (при заданном уровне надежности) не меняют свой знак. Заметим, что столбцы Нижние и Верхние дают нижнюю и верхнюю границу интервальной оценки величины коэффициента регрессии. И если у них будут разные знаки, то прогнозировать по такому уравнению регрессии будет невозможно, поскольку мы будем получать противоречивые оценки.