Владимир Брюков - Как предсказать курс доллара. Расчеты в Excel для снижения риска проигрыша

В результате получим следующий график зависимости «Остатков» от «Остатков с лагом в один торговый день»‑ см. рис.3.1. Судя по тому, что точки на графике разбросаны по кругу в хаотичном порядке, можно сделать вывод об отсутствии автокорреляции в остатках. Построенный на основе графика данных тренд также говорит о низкой величине R2=0,0005, то есть он объясняет лишь 0,05% всей динамики результативной (зависимой) переменной.

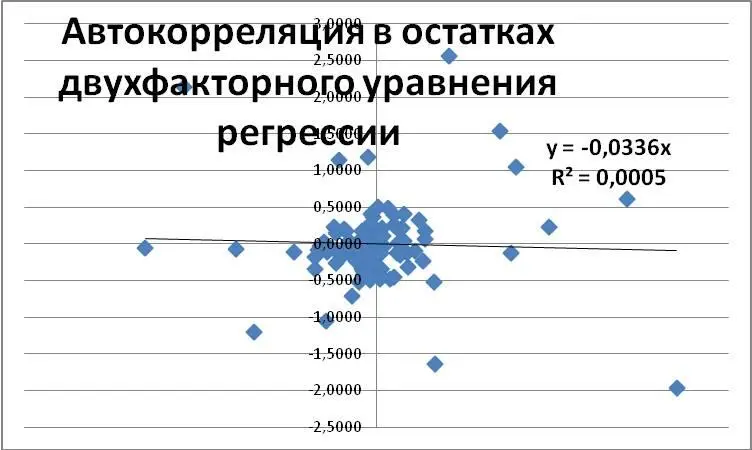
Рис. 3.1

Используя уже апробированный в главах 2 и 3 алгоритм действий № 5 «Как решить уравнение регрессии в Excel», можно решить уравнение регрессии с этими двумя переменными – результативной переменной «Остатки, Y» и независимой переменной «Остатки с лагом в один торговый день, X». В результате выяснится, что как само уравнение регрессии, так и его члены, оказались статистически незначимыми, что подтверждает наш вывод об отсутствии автокорреляции в остатках двухфакторного уравнения регрессии, сделанный на основе графика на рис. 3.1.

После того как мы, согласно алгоритму № 6, провели оценку адекватности однофакторного и двухфакторного уравнений регрессии, посмотрим, какие преимущества имеет каждая из них. С этой целью построим таблицу 3.8.

Судя по этой таблице, единственным и не решающим преимуществом однофакторного уравнения регрессии является его более простая формула. В то время как тремя важными плюсами двухфакторного уравнения регрессии являются: во-первых, более низкая средняя ошибка аппроксимации, во-вторых, более высокий нормированный коэффициент детерминации R2, в-третьих, отсутствие автокорреляции в остатках. Поэтому для прогнозирования курса доллара к рублю по выявленному нами тренду нужно использовать двухфакторное уравнение регрессии.

Таблица 3.8. Сравнение однофакторной и двухфакторной уравнений регрессии

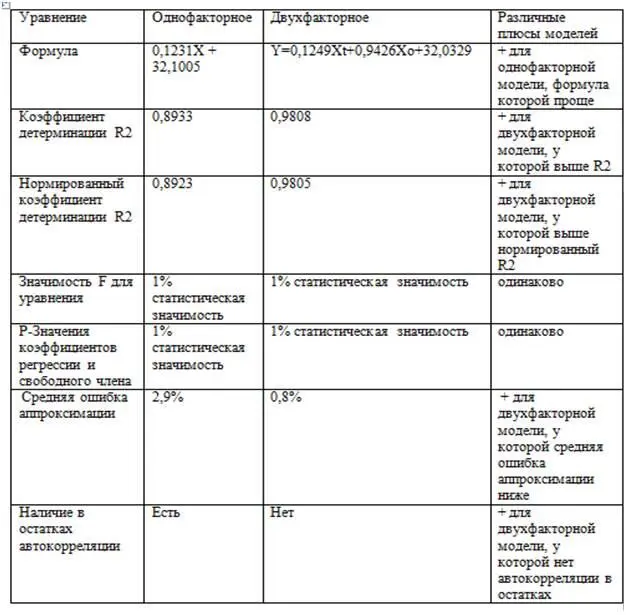
Источник: расчеты автора

Поскольку нам удалось построить – на основе двухфакторного уравнения ‑ вполне адекватную статистическую модель для расчета линейного тренда, теперь займемся составлением прогнозов. Для целей биржевой торговли лучше делать прогноз с горизонтом только в один период времени, что обеспечит его большую точность с учетом имеющейся в момент прогнозирования рыночной информации.

Если бы у нас статистическая модель была построена на данных по итогам ежемесячной, еженедельной, почасовой или 5-минутной торговли, то тогда можно было бы сделать прогноз на конец следующего месяца, недели, часа или пятиминутки и.д. В данном случае, поскольку наша модель построена на основе данных по ежедневным торгам мы будем делать прогноз на следующий день торгов – см. алгоритм № 7. При этом предположим, что данный прогноз делается после завершения торгов в пятницу 28 ноября 2014 года на ближайший после выходных торговый день – на понедельник 1 декабря 2014 года.

Алгоритм № 7 «Составление прогноза по тренду на день торгов»

Шаг 1. Рассчитаем по формуле двухфакторного уравнения регрессии точечный прогноз на 1 декабря 2014 года. С этой целью вставим в двухфакторное уравнение Y=0,1249Xt+0,9426Xo+32,0329 значения независимых переменных на этот торговый день. Заметим, что порядковый номер этого дня =110, а остаток с лагом в один день, полученный после решения однофакторного уравнения, равен для этого дня 3,8052 рублям. В результате наши расчеты приобретут следующий вид:

Y=0,1249*110+0,9426*3,8052 +32,0329 =13,7404+3,5869+32,0329 = 49,3602

Шаг 2. Следовательно, наш точечный прогноз на конец торгов 1 декабря 2014 года равен 49,3602 рублям, а фактический курс по итогам торгов 28 ноября 2014 года составил 49,3220. Таким образом, прогнозируемый на следующий торговый день рост курса доллара к рублю у нас получился равным 0,0382 рублям. С учетом этого небольшого прогнозируемого роста, а также наблюдаемого на рынке достаточно устойчивого повышательного тренда (об этом говорит высокий коэффициент детерминации R2 =0,9808), трейдер может принять решение ‑ занять на прогнозируемый день длинную позицию.

Шаг 3. Точечный прогноз на следующий день можно дополнить интервальным прогнозом для ожидаемого диапазона тренда. С этой целью нужно воспользоваться функциями МИН и МАКС, которые на основе остатков, полученных после решения двухфакторного уравнения регрессии (см. раздел «Остатки» в таблице 3.5) найдут среди них минимальное и максимальное значения.