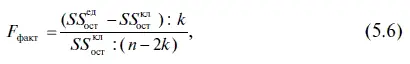Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Проверка нулевой гипотезы идет путем сравнения разницы между суммой квадратов остатков, которую мы получаем, построив уравнение регрессии для единого временного ряда, и суммой квадратов остатков, получаемой при построении уравнения регрессии отдельно для каждого периода этого ряда. При этом в соответствии с методикой, предложенной Г. Чоу, определяется фактическое значение F -критерия и LR -статистики (log likelihood ratio statistic — соотношение статистики логарифмов правдоподобия). Если уровни значимости F -критерия и LR -статистики оказываются меньше 0,05, то тогда нулевая гипотеза о структурной стабильности временн o го ряда отвергается, а следовательно, влияние структурных изменений признается существенным.

В соответствии с данными табл. 5.4 вполне логично предположить, что самые значительные структурные изменения в исследуемом временном ряде могли произойти после самого крупного скачка курса доллара, имевшего место в сентябре 1998 г. Поэтому мы решили выделить в нашем временном ряде период с октября 1998 г. по апрель 2010 г. При этом для корректного проведения теста необходимо, чтобы количество наблюдений в каждом из выделенных периодов временн o го ряда было по меньшей мере равно количеству параметров в оцененной нами статистической модели. Впрочем, это требование соблюдено, поскольку в анализируемой статистической модели всего лишь два параметра, а в самом малом выделенном периоде временного ряда имеется 74 наблюдения.

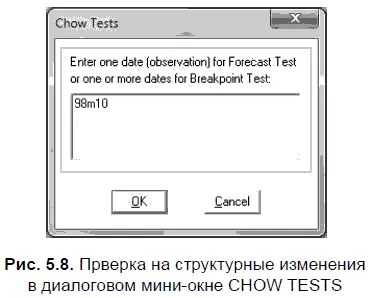
Чтобы в EViews провести тест Чоу на наличие структурной стабильности, в меню оцененного уравнения регрессии необходимо воспользоваться опциями VIEW/STABILITY TESTS/CHOW BREAKPOINT TEST… (смотреть/тесты на стабильность/тест Чоу на структурные изменения). В результате открывается диалоговое мини-окно CHOW TESTS (тесты Чоу), в котором нужно указать конкретное наблюдение, когда произошло предполагаемое структурное изменение во временн о м ряде. В этом случае в мини-окно введено обозначение — 98m10, т. е. указан октябрь 1998 г. (рис. 5.8). Следовательно, можно посмотреть, произошли ли структурные изменения в октябре 1998 г.

После того как мы щелкнули кнопку ОК, в мини-окне CHOWTESTS появился вывод данных по результатам тестирования, которые приведены в табл. 5.10. Поскольку уровни значимости ( Probability ) как F -критерия ( F-statistic ), так и LR -статистики (Log likelihood ratio — соотношения логарифмов правдоподобия) у нас оказались равны нулю, т. е. получились меньше критического значения, равного 0,05, следовательно, нулевая гипотеза о наличии структурной стабильности во временном ряде в октябре 1998 г. отвергается.

После того как была выдвинута нулевая гипотеза о структурной стабильности временн о го ряда, далее нам приходится решать несколько уравнений регрессии USDOLL AR = a × USDOLL AR(−1) + b × USDOLL AR(−2) как относительно единого временного ряда, так и относительно каждого выделенного периода наблюдений. Напомним, что в этом случае мы предположили, что структурная нестабильность возникла в октябре 1998 г., а потому временной ряд нами разделен на два периода: с июня 1992 г. по сентябрь 1998 г. и с октября 1998 г. по апрель 2010 г. Таким образом, мы находим сумму квадратов остатков, полученных как по единому уравнению регрессии для всего временн o го ряда, так и по остальным уравнениям регрессии (назовем их совокупность объединенной кусочно-линейной прогностической моделью) для каждого выделенного периода наблюдений.

Далее складываем суммы квадратов остатков, полученных в объединенной кусочно-линейной прогностической модели, по формуле

После чего находим фактическое значение F -критерия по формуле

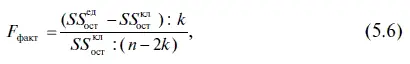
где SS ед ост— сумма квадратов остатков, полученных по единому уравнению регрессии для всего временн о го ряда;