Владимир Брюков - Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Помимо стандартных остатков для анализа выбросов используются также стьюдентизированные остатки, которые представляют собой частное от деления обычного остатка на оценку его стандартного отклонения. Хотя теоретически все случайные ошибки, полученные после решения уравнения регрессии, считаются независимыми и имеющими одну и ту же дисперсию, однако в действительности конкретные остатки в силу своего различенного положения во временном ряду отнюдь не независимы и, следовательно, не имеют одинаковых дисперсий [14] Дрейпер Н., Смит Г. Прикладной регрессионный анализ. С. 190. . Поэтому чтобы учесть эту разницу в дисперсии остатков, их необходимо стьюдентизировать, т. е. оценить с учетом их положения в выборке. Формулу по расчету стьюдентизированных остатков мы дадим далее, а сейчас приведем алгоритм действий, с помощью которого можно быстро получить стьюдентизированные остатки. Правда, в Excel такая возможность отсутствует, но в последних версиях EViews эту процедуру можно реализовать с помощью статистики влияния остатков (INFLUENCE STATISTICS). Чтобы уяснить, как это делается, надо прочитать алгоритм действий № 17.

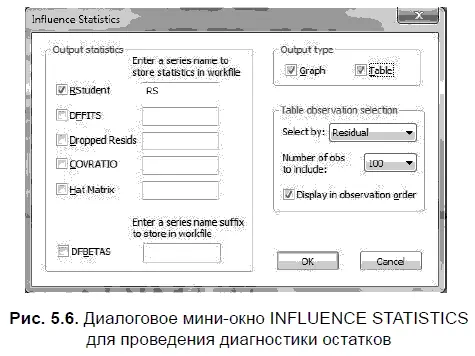
После решения уравнения регрессии (на основе рыночных данных по курсу доллара за период с июня 1992 г. по сентябрь 1998 г.) в строке EQUATION выбираем опции VIEW/STABILITY DIAGNOSTICS/INFLUENCE STATISTICS. В результате на экране появляется диалоговое мини-окно INFLUENCE STATISTICS, которое нужно соответствующим образом заполнить, чтобы провести диагностику остатков (рис. 5.6). Чтобы получить как графический, так и табличный вариант по статистике влияния остатков в параметре OUTPUT TYPE (тип выходной статистики), следует установить опции GRAPH (график) и TABLE (таблица). Далее в параметре OUTPUT STATISTICS (выходная статистика) ставим галочку у опции RSTUDENT (стьюдентизированные остатки) и рядом пишем RS — название файла, который будет помещен в рабочий файл.

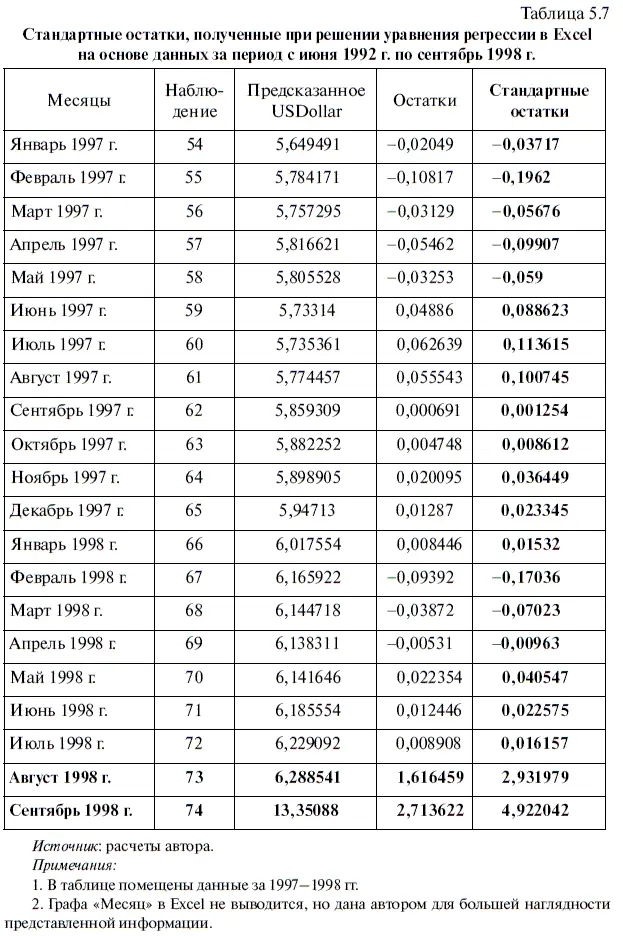
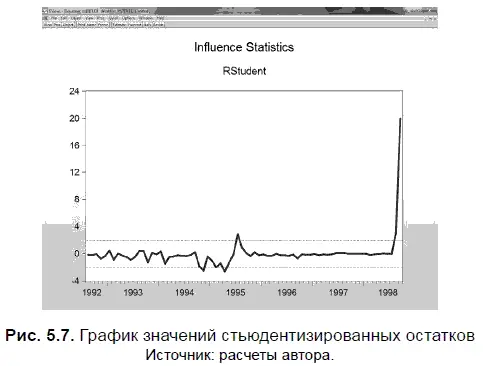
В результате шага 1 получены диаграмма (она приведена на рис. 5.7) и табл. 5.8. Интерпретация диаграммы довольно проста, поскольку на ней представлен график значений стьюдентизированных остатков, который с обеих сторон выделен пунктирной линией и обозначает область допустимых значений, равных ± 2. Когда стьюдентизированные остатки выходят за пределы этой пунктирной линии, в этом наблюдении их можно считать выбросами. Легко заметить, что особенно велик стьюдентизированный остаток, полученный в сентябре 1998 г.

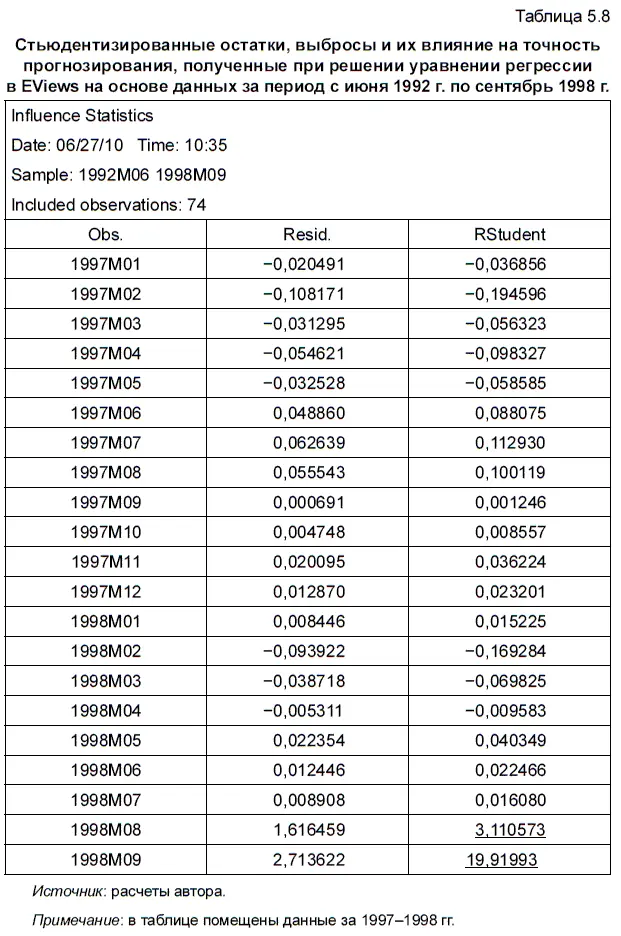
В таблице 5.8 приведена часть полученных с помощью EViews значений стьюдентизированных остатков (за период с января 1997 г. по сентябрь 1998 г.). При этом стьюдентизированные остатки, которые считаются выбросами (их величина больше или меньше 2), при выводе итогов обозначаются EViews красным шрифтом (в таблице они подчеркнуты). При этом область допустимых значений определяется с помощью уже известной нам t -статистики. В частности, выбросами считаются остатки, которые получены не только в сентябре, но и в августе 1998 г. Если сравнить стандартные остатки из табл. 5.7 со стьюдентизированными остатками, то легко заметить, что значения последних — за счет выросшей дисперсии между наблюдениями — наиболее сильно отличаются от значений первых для августа и сентября 1998 г.

Теоретически все случайные ошибки предполагаются независимыми и имеющими одну и ту же дисперсию σ 2, однако в действительности конкретные остатки отнюдь не независимы и, следовательно, не имеют одинаковых дисперсий. В действительности дисперсия остатков зависит не только от величины σ 2, но и от h i— i- го диагонального элемента матрицы вида Х t(Х`Х) -1Х t , с которой мы уже познакомились в главе 3.