Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

В современной России, когда уже нет цензуры и идеологического давления, побуждавшего недобросовестных авторов доказывать, что «Россия — родина слонов», а отечественные работы являются обязательно «основополагающими», имеются все условия для объективного освещения истории науки. К сожалению, советский стиль «исторических» изысканий еще не забыт, и мне недавно пришлось с этим столкнуться. Последнее и послужило мотивом для того, чтобы написать настоящую статью.

После опубликования книги [2] я физикой плазмы активно не занимался и поэтому не обратил внимания на появление в 1997 г. в журнале «Физика плазмы» под рубрикой «Из истории науки» статьи А. Ф. Александрова и А. А. Рухадзе [3]. Об этой статье узнал лишь в июле 2000 г. из подкинутой мне в ФИАНе рукописи под названием «Ландау и другие». В качестве автора указан М. Ковров, но адреса нет, а сочинение это антисемитского типа, поэтому, вероятно, это анонимка. Тем не менее я указываю здесь на эту рукопись, поскольку нецензурных слов она не содержит и в современных условиях может оказаться опубликованной. Конечно, цитировать господина (или товарища) Коврова не собираюсь, укажу лишь, что статья Александрова и Рухадзе широко используется в, ней для «доказательства» того, как Л. Ландау и другие травили А. А. Власова. И действительно, Александров и Рухадзе беззастенчиво искажают содержание критики некоторых работ А. А. Власова, изложенной в статье В. Л. Гинзбурга, Л. Д. Ландау, М. А. Леонтовича и В. А. Фока (далее ГЛЛФ) и опубликованной в 1946 г. [4].

Чтобы читателям была ясна ситуация, придется сделать несколько предварительных замечаний. Еще в 1920-е гг. был достигнут немалый прогресс в изучении газоразрядной плазмы — ионизованного газа малой плотности. Известны работы Ленгмюра и в особенности статья Тонкса и Ленгмюра [5], опубликованная в 1929 г. Эти авторы самосогласованным образом рассматривали движение частиц (электронов и ионов) и уравнения электромагнитного поля (уравнения Максвелла) и, в частности, понимали, что в плазме могут распространяться не только поперечные, но и продольные волны (колебания) с характерной циклической плазменной частотой ω p , причем ω p 2= 4 πe 2 N/m (здесь e и m — заряд и масса электрона, а N — концентрация электронов). В статье [5] рассмотрен и вопрос о вкладе ионов, а также некоторые другие, но кинетические уравнения для частиц не использовались. Последнее, на первый взгляд, может вызвать удивление, поскольку кинетическое уравнение Больцмана широко применялось для описания процессов в газах уже много десятилетий до появления этой работы. По всей вероятности, дело в том, что в плазме, в отличие от неионизованных газов, совсем непросто записать выражение для нетривиальной части уравнения Больцмана, а именно для столкновительного члена (интеграла столкновений) St f (здесь и ниже пользуюсь обозначениями, принятыми в книге [6]). С учетом этого члена уравнение Больцмана для функции распределения частиц f ( t, r, p ) имеет вид

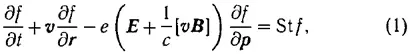
где v = p/m — скорость частиц, E и B — напряженности электрического и магнитного полей (частицы считаем электронами, их заряд равен е). При рассмотрении процессов переноса (электропроводности, теплопроводности и т. п.) поля E и B обычно считаются внешними, заданными, и, как было сказано, главным является уточнение смысла интеграла столкновений St f . Для плазмы эта нетривиальная задача была в хорошем приближении решена Л. Д. Ландау в 1936 г. [7] (см. [6, § 41]). Имеется, однако, круг вопросов, для анализа которых поля E и B нельзя считать заданными, а нужно учитывать также и поля, создаваемые частицами самой плазмы. Простейшая задача такого типа — распространение волн в плазме. Для ее решения, да и в более широком плане, А. А. Власов в опубликованной в 1938 г. работе [8] предложил использовать кинетическое уравнение с согласованным полем. В этом методе интеграл столкновений St f вообще отбрасывается, но поля E и B считаются полными, т. е. учитываются также поля, созданные частицами самой плазмы. В подобных условиях поля E и B подчиняются уравнениям Максвелла. В простейшем случае, когда речь идет о продольном поле, в линейном приближении нужно использовать уравнения