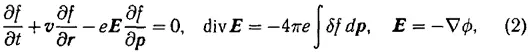
где положено f = f 0+ δf, f 0— невозмущенная функция распределения и δf — малая добавка; при этом в (2) для простоты считается, что функция /о отвечает состоянию, в котором заряд и ток равны нулю (разумеется, заряд электронов компенсируется зарядом ионов). Таким образом, для потенциала получается уравнение Пуассона ∆ ф = 4 πe ʃ δfdp . Уравнения (2) или более общие для полей E и B , подчиняющихся уравнениям Максвелла, в литературе нередко называют уравнениями Власова. Нисколько не умаляя заслуги Власова, применившего такое самосогласованное приближение, я не вижу разумных оснований для подобного словоупотребления, ибо речь идет об укороченном уравнении Больцмана и уравнениях Максвелла (или уравнении Пуассона). Любопытно, что А. А. Рухадзе в своей книге [9], о которой речь пойдет ниже, на с. 73 похваляется тем, что всячески популяризировал термин «уравнение Власова». Вместе с тем в учебнике [10], одним из авторов и редактором которого является тот же Рухадзе, посвященном уравнениям типа (2), параграф 3. 2 назван «Кинетическое уравнение с самосогласованным полем». Думаю, что такое название правильнее всего. Но, разумеется, вопрос о терминологии не имеет особого значения, и, когда говорят «уравнения Власова», физики понимают, о чем идет речь, а по сути дела только это и важно. Я позволил себе сделать это отступление потому, что в книге [9] на с. 73 Рухадзе утверждает также, что я якобы «всеми фибрами своей души не любил Власова» и оказывал «яростное сопротивление» использованию термина «уравнение Власова». И то и другое, как и многое в [9], совершенно не соответствует действительности и является плодом богатого и, к сожалению, весьма недоброкачественного воображения Рухадзе [57] «Клевещите, клевещите, что-нибудь да останется». Это известное выражение правильно, к сожалению, отражает нравы, нередко царящие в человеческом обществе. Замечу поэтому, что лишь в 1938–1940 гг., тогда аспирант на физфаке МГУ, я был формально знаком с А. А. Власовым. Но ни тогда, ни позже никогда не участвовал в каких-либо дискуссиях с ним. Никогда не приходилось мне писать какие бы то ни было отзывы о работах или деятельности Власова, если не считать соавторства в статье ГЛЛФ [4]. Работу Власова [8] я в своей книге [2], естественно, цитирую, причем без всякой критики.
.
Вернемся, однако, к существу дела. Полагая в (2) функцию δf пропорциональной exp[ i ( kr— ωt )]> находим

Как хорошо известно, из электродинамики, для продольных волн (см., напр., [2, 7, 10, 11])

где ε l — продольная диэлектрическая проницаемость, связывающая для продольного поля поляризацию P = (( ε l - 1)/4π) E полем E . Но поляризация P выражается через δf соотношением (см., напр., [7, § 29])

Подставляя сюда решение (3), приходим к дисперсионному соотношению (4) в виде
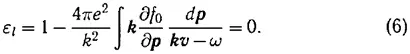
Это выражение Власов и получил, но, по сути дела, проигнорировал имеющуюся в (6), вообще говоря, расходимость интеграла при

Поэтому Власов пришел к выводу о существовании в равновесной (максвелловской) плазме незатухающих плазменных волн, для которых

где T — температура и k B — постоянная Больцмана.
На самом же деле в указанных условиях волны, как показал Ландау [12], затухают. Это связано именно с полюсом в выражении (6), имеющим место при условии (7). Затухание Ландау играет очень большую роль в физике плазмы и широко исследовалось в различных случаях (см. [6, 11]). Особенно важно отметить, что Ландау, как и Власов, ограничился рассмотрением плазмы в предположении, что функция f 0в (6) является максвелловской. В общем же случае, рассмотренном позже другими авторами, затухание может отсутствовать — для этого достаточно, чтобы функция дf 0/ д P равнялась нулю в полюсе (7) и интеграл был конечен.
Читать дальше

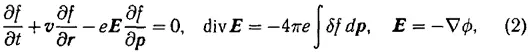








![Коллектив авторов Биографии и мемуары - Ковалиная книга. Вспоминая Юрия Коваля [второе издание, исправленное и дополненное]](/books/430445/kollektiv-avtorov-biografii-i-memuary-kovalinaya-kn-thumb.webp)






