А. А. Власов на основе приведенной системы уравнений в пренебрежении парными столкновениями исследовал малые линейные колебания плазмы в отсутствие внешних источников и внешних полей. При это он показал, что в такой изотропной плазме существуют чисто продольные (в которых Е = — 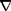 Ф) и чисто поперечные (в которых div E = 0) волны, и получил для них в общем виде дисперсионные соотношения, связывающие частоту и и волновой вектор k для возмущения вида exp( —iωt + i kr ). Здесь приведем результаты анализа только чисто электронных продольных колебаний, поскольку именно они перекликаются с результатами работ Л. Д. Ландау.
Ф) и чисто поперечные (в которых div E = 0) волны, и получил для них в общем виде дисперсионные соотношения, связывающие частоту и и волновой вектор k для возмущения вида exp( —iωt + i kr ). Здесь приведем результаты анализа только чисто электронных продольных колебаний, поскольку именно они перекликаются с результатами работ Л. Д. Ландау.
Проведенный А. А. Власовым анализ дисперсионного уравнения для малых продольных колебаний изотропной электронной плазмы с максвелловской равновесной функцией распределения по скоростям показал, что в пренебрежении парными столкновениями частиц в области фазовых скоростей, превышающих тепловую скорость электронов, такие колебания не затухают и обладают следующим законом дисперсии:

где и ω p — известная со времен И. Ленгмюра плазменная (электронная ленгмюровская) частота, а 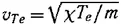 — тепловая скорость электронов. Наличие спектра высокочастотных электронных колебаний с малой групповой скоростью
— тепловая скорость электронов. Наличие спектра высокочастотных электронных колебаний с малой групповой скоростью

хорошо согласовывалось с известными экспериментальными результатами И. Легмюра и Л. Тонкса [8]. Подтверждением правильности теории А. А. Власова следует считать также то, что медленные продольные колебания в чисто электронной плазме оказались невозможными. Именно, в области v φ = ω/k << v Te поле таких колебаний экранируется, причем размер экранировки определяется дебаевским радиусом, что согласуется с глубиной дебаевской экранировки поля статического заряда в плазме (7), полученной Л. Д. Ландау из чисто термодинамических соображений [52] Следует отметить, что в цитируемой работе И. Легмюра и Л. Тонкса в рамках гидродинамического описания была развита идеология самосогласованного поля и, более того, получены спектры (12) (с небольшой неточностью: вместо коэффициента 3 в поправочном слагаемом они получили множитель 1) и дебаевская экранировка низкочастотного продольного поля. Ими же было показано, что малые возмущения в плазме не апериодически затухают со временем, а колеблются с частотой ω p и лишь слабо затухают вследствие столкновений электронов.
.
Вместе с тем вызывало некоторую неудовлетворенность отсутствие затухания колебаний, хотя в приближении самосогласованного поля взаимодействие частиц учитывалось. Сам А. А. Власов в этом ничего плохого не видел. Более того, парную столкновительную релаксацию, которая, согласно теории Л. Д. Ландау, определяется частотой электрон-ионных столкновений

он считал пренебрежимо малой, поскольку
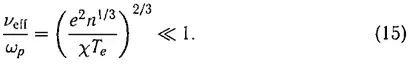
Более существенным А. А. Власову представлялось дисперсионное расплывание. Оценивая исходя из формулы (12) время расплывания τ g неоднородности с размером 1/ k , находим, что
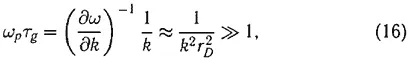
т. е. это время велико по сравнению с периодом колебаний. Причем роль столкновений определяется величиной ν eff τ g , которая есть произведение малого параметра (15) на большой параметр (16).
4. В [2] Л. Д. Ландау резко отрицательно отреагировал на отсутствие в теории А. А. Власова диссипации малых колебаний при пренебрежении парными столкновениями. Считая уравнение Власова применимым для описания электронных колебаний плазмы, он тем не менее писал: «Власов искал решения вида exp( —iωt + i kr ) и определял зависимость частоты ω от волнового вектора k . В действительности вообще не существует никакой определенной зависимости ω от k , и при заданном значении k возможны произвольные ω ». Решая, как и А. А. Власов, начальную задачу для малых колебаний, Л. Д. Ландау приходит к тому же дисперсионному уравнению [53] Ландау вообще не воспринимал введение дисперсионного уравнения, что особенно резко прозвучало в статье [5].
Читать дальше

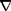 Ф) и чисто поперечные (в которых div E = 0) волны, и получил для них в общем виде дисперсионные соотношения, связывающие частоту и и волновой вектор k для возмущения вида exp( —iωt + i kr ). Здесь приведем результаты анализа только чисто электронных продольных колебаний, поскольку именно они перекликаются с результатами работ Л. Д. Ландау.
Ф) и чисто поперечные (в которых div E = 0) волны, и получил для них в общем виде дисперсионные соотношения, связывающие частоту и и волновой вектор k для возмущения вида exp( —iωt + i kr ). Здесь приведем результаты анализа только чисто электронных продольных колебаний, поскольку именно они перекликаются с результатами работ Л. Д. Ландау.
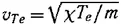 — тепловая скорость электронов. Наличие спектра высокочастотных электронных колебаний с малой групповой скоростью
— тепловая скорость электронов. Наличие спектра высокочастотных электронных колебаний с малой групповой скоростью

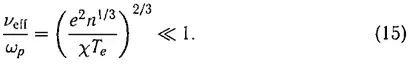



![Коллектив авторов Биографии и мемуары - Ковалиная книга. Вспоминая Юрия Коваля [второе издание, исправленное и дополненное]](/books/430445/kollektiv-avtorov-biografii-i-memuary-kovalinaya-kn-thumb.webp)






