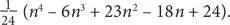Алекс Беллос - Красота в квадрате

[5]Если количество точек на линии окружности равно n , то количество секторов рассчитывается по формуле

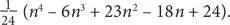
[6]В отличие от Фреге, некоторые специалисты по философии математики считают, что утверждение «отрицание отрицания утверждения А есть утверждение А» содержит глубокое противоречие.

[7]Douglas R. Hofstadter, Metamagical Themas, Basic Books, 1996.

[8]Martin Gardner, Logical Paradoxes, The Antioch Review, 1963.

[9]John Allen Paulos, I Think, Therefore I Laugh, Penguin, 2000.

[10]Одна из главных целей теории множеств состояла в том, чтобы доказать полноту математики. Другими словами, чтобы доказать, что, если теорема истинна, значит, она доказуема в рамках данной системы. Однако в 1931 году Курт Гедель доказал, что на самом деле это не так: в любой системе, достаточно мощной, чтобы включать в себя арифметику, обязательно найдутся утверждения, которые невозможно ни доказать, ни опровергнуть. Работа Геделя оказала существенное влияние на математическую философию, поскольку ограничила сферу действия логики в качестве основы для математики.

[11] Николя Бурбаки . Теория множеств. М. : Либроком, 2010. Интересно то, что Бурбаки ни разу не упоминает имя Курта Геделя (см. предыдущее примечание).

[12]Полдавия (фр. Poldèvie ) — это шуточная страна, придуманная в 1929 го­ду одним французским журналистом с правыми убеждениями и упомянутая в письме членам парламента левого крыла, в котором он от имени угнетенного народа Полдавии просит их вмешаться. После того как группа Бурбаки сделала Полдавию своей родиной, эта шутка начала часто появляться в работе нескольких французских писателей послевоенного периода. Профессор французского языка и литературы Принстонского университета и отец автора этой книги Дэвид Беллос сказал, что это «редкий пример того, как математический юмор стал темой литературных произведений».

[13]Maurice Mashaal, Bourbaki, American Mathematical Society, 2006.

[14]A. R. D. Mathias, A term of length 4,523,659,424,929, Synthese, 2002.

[15]Bob Moon, Who Controls the Curriculum? The story of New Maths 1960–1980, International Perspectives in Curriculum History, 1987.

[16]В настоящее время насчитывается более десятка систем для проверки доказательств; самые известные — Coq, HOL Light, Isabelle и Mizar. Систему Mizar в 1970-х годах начали разрабатывать в Польше; ее пользователи утверждают, что она содержит самую крупную логически связную базу формализованных доказательств.

[17]Имеется в виду, что можно доказать все математические утверждения, которые в принципе доказуемы (см. примечание о Геделе).

[18]Steven G. Krantz, The Proof is in the Pudding, Springer, 2011.

ГЛАВА 10

[1] Теорема.Если для нахождения простых чисел просеиваются n чисел, то в этом случае достаточно проанализировать на наличие простых чисел числа, не превышающие √ n .

Доказательство.Представьте, что вы перебрали все простые числа до √ n включительно, но осталось незачеркнутым непростое число m , которое находится между √ n и n . Число m не является простым, тогда у него должны быть простые множители, причем больше √ n . (Иначе это число было бы вычеркнуто на предыдущих этапах.) Однако произведение двух или более чисел, больших √ n , — это число, которое больше n , а значит, число m не может быть меньше n , что и требовалось доказать29.

[2]Одним из его любимых названий было: «Не звоните нам, мы сами вам позвоним!»

[3]Martin Gardner, Mathematical Games: The Entire Collection of His Scientific American Columns, CD, 2005.

[4]Если кто-то захочет сыграть в игру «Жизнь» (а я настоятельно рекомендую сделать это), лучше всего воспользоваться программой Golly, которую можно скачать здесь: golly.sourceforge.net.

[5]Steven Levy, Hackers, O’Reilly Media, 2010.

[6]Первое решето Эратосфена создал Дин Хикерсон в 1991 году. Решето, которое упомянуто здесь, — это усовершенствованная версия, разработанная Джейсоном Саммерсом в 2005 году.

[7]William Poundstone, The Recursive Universe, Oxford University Press, 2005.

[8]Когда эта книга уже ушла в печать, американский «жизнелюб» (любитель игры «Жизнь») Дэйв Грин объявил о получении новой самовоспроизводящейся фигуры, в которой количество живых клеток конструктора сократилось с 16 229 (как у «Джемини») до 256. Он назвал эту конфигурацию «репликатор Джеминоид», поскольку в нем используется ряд элементов той же технологии, что и у «Джемини». Однако, в отличие от «Джемини», у этой фигуры всего один конструктор, который выживает после создания копии, а не два, которые разрушаются, выполнив свою функцию. Репликатор «Джеминоид» порождает точную копию, которая порождает очередную точную копию и так далее до бесконечности, создавая линию потомков, распространяющуюся по всей сетке. Учитывая, что конструктор состоит из такого малого количества живых клеток, это облегчает построение новых конфигураций. Дэйв надеется на то, что технология «Джеминоида» приведет к появлению множества репликаторов новых типов.