Алекс Беллос - Красота в квадрате

[20]Birte Englich, Thomas Mussweiler and Fritz Strack, Playing Dice With Criminal Sentences: The Influence of Irrelevant Anchors on Experts Judicial Decision Making, Personality and Social Psychology Bulletin, 2006.

[21]Мой интернет-опрос (сайт favouritenumber.net) начался в 2011 году. На титульной странице сайта было его описание, после которого следовало два предложения: «Мое любимое число — …» и «Я выбираю его, потому что…» Респонденты могли сформулировать свои ответы словами или просто назвать цифры. Результаты, о которых идет речь на страницах этой книги, получены в ходе обработки 33 516 ответов; из них 3491 ответ был неопределенным или вообще отсутствовал. К моменту сдачи книги в печать в опросе приняли участие уже 42 000 респондентов.

[22]Eviatar Zerubavel, The Seven Day Circle, Free Press, 1985.

[23]Georges Ifrah, The Universal History of Numbers, John Wiley & Sons, 2000.

[24]Michael Kubovy and Joseph Psotka, The predominance of seven and the apparent spontaneity of numerical choices, Journal of Experimental Psychology: Human Perception and Performance, 1976.

[25]Существует всего восемь двузначных нечетных чисел от 1 до 50, состоящих из разных цифр, причем число 15 упомянуто в описании задачи, поэтому респондент вряд ли назовет его. Авторы книги The Psychology of the Psychic (Prometheus Books, 1980) Дэвид Маркс и Ричард Кэмменн разыграли этот трюк на занятии по психологии — и больше трети студентов выбрали число 37. Результаты были такими: число 37 (35 процентов), 35 (23), 17 (10), 39 (10), 19 (9), 31 (5), 13 (5), другие числа (3).

[26]Dan King and Chris Janiszewski, The Sources and Consequences of the Fluent Processing of Numbers, Journal of Marketing Research, 2011.

[27]Marisca Milikowski, Knowledge of numbers: A study of the psychological representation of the numbers 1–100, PhD thesis at the University of Amsterdam, 1995.

ГЛАВА 2

[1]Domesday Book: A Complete Translation, Penguin Classics, 2003.

[2]Simon Newcomb, Note on the Frequency of Use of the Different Digits in Natural Numbers, American Journal of Mathematics, 1881.

[3]Frank Benford, The law of anomalous numbers, Proceedings of the American Philosophical Society, 1938.

[4]

Число

1

2

3

4

5

6

7

8

9

Закон Бенфорда

30,1

17,6

12,5

9,7

7,9

6,7

5,8

5,1

4,6

Население округов

30,2

18,8

12,2

9,9

7,1

6,3

5,7

4,8

5,0

Доходы компаний

30,2

17,7

12,5

9,8

7,9

6,7

5,7

5,1

4,5

Сведения о населении округов США взяты из отчетов о результатах опроса американского общества (American Community Survey) за 2007–2011 годы. Финансовые данные — итог анализа 1,4 миллиона единиц информации из системы Compustat, выполненного Джайлан Ванг.

[5]Scott de Marchi and James T. Hamilton, Assessing the accuracy of self-reported data: an evaluation of the toxics release inventory, Journal of Risk and Uncertainty, 2006; Walter R. Mebane Jr., Fraud in the 2009 Presidential Election in Iran?, Chance, 2010; Malcolm Sambridge et al., Benford’s law in the natural sciences, Geophysical Research Letters, 2010.

[6]Miles L. Hanley, Word Index to James Joyce’s Ulysses, University of Wisconsin Press, 1953.

[7]George Kingsley Zipf, Human Behavior and the Principle of Least Effort, Addison-Wesley, 1949.

[8]Слово, которое появляется в тексте только один раз, обозначается термином «гапакс легоменон» (от древнегреческого hapax legomenon — «названный только раз»). Этот термин звучит как имя персонажа одной из историй об Астериксе или название скандинавской группы в стиле Death Metal. В издании данной книги на английском языке есть только одно такое слово.

[9] Ричард Кох . Принцип 80/20. М. : Эксмо, 2012.

[10]Fredrik Liljeros et al., The web of human sexual contacts, Nature, 2001.

[11]N. Johnson et al., From old wars to new wars and global terrorism, arXiv:physics/0506213, 2005.

[12]Joao Gama Oliveira and Albert-Laszlo Barabasi, Human dynamics: Darwin and Einstein correspondence patterns, Nature, 2005.

[13]Takashi Iba et al., Power-Law Distribution in Japanese Book Sales Market, Fourth Joint Japan-North America Mathematical Sociology Conference, 2008.

[14]Mark Buchanan, Ubiquity, Weidenfeld & Nicolson, 2000.

[15]Albert-Laszlo Barabasi, Linked, Perseus, 2002; Albert-Laszlo Barabasi, Bursts, Penguin, 2010.

[16]Michael P. H. Stumpf and Mason A. Porter, Critical Truths About Power Laws, Science, 2012; Aaron Clauset, Cosma Rohilla Shalizi, and M. E. J. Newman, Power-Law Distributions in Empirical Data, SIAM Review, 2009.

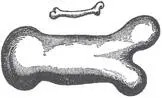
[17]В книге Discourses and Mathematical Demonstrations Relating to Two New Sciences («Беседы и математические доказательства двух новых наук») Галилей сделал следующий набросок двух костей — маленькой и тонкой, а также большой и толстой. Он писал, что у большого животного большая кость «выполняла бы ту же функцию, что и маленькая кость у маленького животного».

Компания по выпуску игрушек для собак Nylabone продает нейлоновые жевательные кости, имеющие точно такую же форму, как на представленном ниже рисунке. В компании утверждают, что эти кости (получившие название Galileo) — «самые прочные жевательные кости для собак».

[18]Melanie Mitchell, Complexity: A Guided Tour, Oxford University Press, 2009.

[19]Geoffrey B. West, James H. Brown, and Brian J. Enquist, A General Model for the Origin of Allometric Scaling Laws in Biology, Science, 1997.

[20]Luis M. A. Bettencourt et al., Growth, innovation, scaling, and the pace of life in cities, PNAS, 2007.