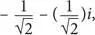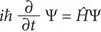Алекс Беллос - Красота в квадрате

[9]Еще одно решение уравнения x 2= i выглядит так:

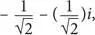
что обратно решению, приведенному в тексте.

[10]Ed Leibowitz, The Accidental Ecoterrorist, Los Angeles Magazine, 2005.

[11]Джеймс Томсон, с которым мы встретимся в главе 8, ввел термин «радиан» в 1873 году, хотя сама концепция была известна к тому времени уже полтора столетия.

[12]Волновое уравнение Шредингера выглядит так:

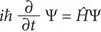
где i = √–1, ћ — приведенная константа Планка, Ψ — волновая функция квантовой системы, Ĥ — оператор Гамильтона.

[13]Melanie Bayley, Algebra in Wonderland, The New York Times, 2010.

[14]John C. Baez and John Huerta, The Strangest Numbers in String Theory, Scientific American, 2011.

[15]Bertrand Russell, The Study of Mathematics, Mysticism and Logic: And Other Essays, Longman, 1919. Бертран Рассел — единственный математик мирового уровня , получивший Нобелевскую премию по литературе. Однако диплом по математике был и у Александра Солженицына (Нобелевская премия за 1970 год), и у Джона Максвелла Кутси (2003 год).

[16]Дэйв Болл публиковал свои статьи не в журнале, а на форуме, посвященном фракталам: groups.google.com/­forum/­?hl=en#!­topic/­sci.math/­jHYDf-Tm0-8.

ГЛАВА 8

[1]В 2001 году правительство Норвегии учредило ежегодную Абелевскую премию, названную в честь норвежского математика Нильса Хенрика Абеля (1802–1829). Ее денежный размер составляет около 1 миллиона долларов. Хотя эта премия аналогична Нобелевской по размеру и скандинавскому происхождению, она пока не заслужила такой репутации, как Филдсовская премия.

[2]gowers.wordpress.com.

[3]Plutarch, Life of Marcellus, цитируется по материалам онлайнового архива истории математики MacTutor.

[4]Carl B. Boyer, The History of the Calculus and Its Conceptual Development, Dover, 1959.

Большой треугольник строится таким образом, чтобы касательная, проведенная в его нижней вершине, была параллельна исходной прямой. Точно так же при построении каждого нового треугольника его вершина размещается так, чтобы касательная в этой точке была параллельна противоположной стороне.

[5]Ernst Sondheimer and Alan Rogerson, Numbers and Infinity, Dover, 2006.

[6]James Gleick, Isaac Newton, Harper Perennial, 2003.

[7]Ian Stewart, 17 Equations that Changed the World, Profile Books, 2012; Charles Seife, Zero, Souvenir Press, 2000.

[8]A. Rupert Hall, Philosophers at War, Cambridge University Press, 2002.

[9]Augustus De Morgan, A Budget of Paradoxes, 1872.

[10]Функция f ( t, x, v ) — это функция плотности вероятностей, которая определяет вероятность того, что частица окажется рядом с х при скорости v в момент времени t . Символом ∇ обозначается градиент, но применительно к нескольким переменным. Cédric Villani, Théorème vivant, Grasset, 2012.

[11]The Railroad Gazette (now Railway Age), 1880, цитируется по изданию: Halsey G. Brown, The History of the Derivation of the AREMA Spiral, arema.org.

[12]Клотоида — это кривая, кривизна которой пропорциональна длине. В алгебраической форме это можно записать так: кривизна = ks , где k — произвольная константа, s — расстояние вдоль кривой от начала координат. Бельгийский математик Фрэнки Диллен создал целый новый класс спиралей, рассчитывая их кривизну по формуле, представляющей собой многочлен с переменной s . (Многочлен, или полином, — это выражение, состоящее из переменных и степеней переменных, в котором используются только операции сложения, вычитания и умножения.) Диллен назвал эти кривые «полиномными спиралями». Они очень красивы; одна из любимых кривых Диллена — так называемая спираль Пикассо.

Кривизна = 10 (−45 + 51 s −18 s 2+ 2 s 3)

[13]Joe Moran, On Roads, Profile Books, 2009.

[14]Robert Cartmell, The Incredible Scream Machine, Amusement Park Books, 1987; Chemin de Fer Aerien, La Nature, 1903.

Прежде чем открыть для публики аттракцион с мертвой петлей, было проведено три испытания: первое — с обезьянами в качестве пассажиров, второе — с грузом тяжелее веса крупного человека и третье — с участием акробата.

[15]George Berkeley, The Analyst: Or, a Discourse Addressed to an Infidel Mathematician, 1734.

ГЛАВА 9

[1]Steven G. Krantz, The Proof is in the Pudding, Springer, 2011.

[2]Martin Gardner, Mathematical Games: The Entire Collection of His Scientific American Columns, CD, 2005.

[3]Львов (укр. Львів) находится сейчас на территории Украины.

[4]В период написания книги лучшими кандидатами на звание самого скучного числа было число 224, которое являлось в то время наименьшим числом, не имеющим своей страницы в «Википедии», и 14 228, наименьшее число, которого не было в онлайновой Энциклопедии целочисленных последовательностей (Encyclopedia of Integer Sequences). Но поскольку об этих числах написано здесь, они стали интересными.