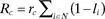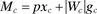Bruce Mesquita - The Logic of Political Survival

We assume that everyone shares a common discount value (δ) in calculating the worth of future benefits. 3Those not in the winning coalition receive no private goods, while those in the coalition each receive the same share of private goods. 4We focus on the following specific utility function— V ( x , g , y , l ) = x ½+ g ½+ y ½+ l ½—for numerical examples, but in the appendix we do not assume such a specific form. 5

The incumbent leader receives a payoff of Ψ + R L - M L , where R L represents total government revenues collected during the current period under the incumbent’s leadership and M L represents the incumbent’s total expenditures on public and private goods ( M L = px L + | W L | g L ) in that period if she survives in office. The incumbent’s payoff if she fails to retain her office is 0. The inherent value of holding office is Ψ ≥ 0. This term plays no consequential role in any of our general results, but it does play some part when we turn to analyzing an important linkage between domestic politics and foreign affairs. For now, we note that the value of office in our model can be 0, though it cannot be negative. That is, all else being equal, leaders want to be in office. The intrinsic value of office (Ψ) reflects the idea that some people derive psychological or symbolic value simply from being in power.

The important aspect of the leader’s utility in terms of the results from our theory is the term R - M L . This term reflects the surplus resources the incumbent can keep for her own discretionary use. These slack resources can be thought of as the opportunity the incumbent has to engage in kleptocracy—that is, theft of the state’s wealth for personal use—or as the cushion the incumbent has against challenges by political rivals. This surplus can be used for any purpose the incumbent chooses. Public-spirited leaders might spend the surplus on pet projects designed to enhance public welfare, or they might retain the surplus as insurance against the chance of political trouble if they risk losing support from members of the winning coalition. Additionally, they might place the surplus in an offshore account to provide for their own personal welfare.

If the challenger succeeds in coming to power, his payoff in the initial, transition period in power equals Ψ + R C - M C , where

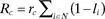
and

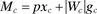
In subsequent periods after the transition, the challenger becomes the new incumbent, and so his payoff is as specified above for the incumbent leader. If the challenger fails to attain office his payoff is 0. Finally, the leader, whether she be the former incumbent or the newly acceded challenger, learns her affinity for members of the selectorate. Of course, if it is the incumbent who survives, she already had this information. In contrast, this information is useful for a former challenger, who having emerged from a position of obscurity, has not had past opportunities to learn who he would ideally like in his future coalitions. With these payoffs in mind, the time line of a round of the leadership selection game is given in box 3.1.

Equilibria of the Selectorate Model

We now describe a Markov perfect equilibrium (MPE; see Fudenberg and Tirole 1991, chap. 13) in which the incumbent always survives in each period, with the incumbent choosing the selectors for whom she has the highest affinity to be members of her coalition. Of course we could introduce uncertainty into the model so that the incumbent would not necessarily be reselected. We do just that in chapter 7 when our attention turns to what leaders do to improve their prospects for political survival. For now, however, our primary interest is in identifying the optimal policy choices—tax rates, public-goods provisions, private-goods provisions, total spending levels, and individual labor efforts—that result from the leader’s efforts to stay in office. It is easy enough to see how an incumbent might lose office by spending too much or too little on public or private goods or by taxing at the wrong rate. It is harder to see how the optimal tax rate and spending allocations relate to coalition and selectorate size. We will show how these optimal levels depend on the size of the winning coalition, the size of the selectorate, and the ratio between the two.

Box 3.1The time line

1. The incumbent leader picks a coalition, W L , of size W from the members of the selectorate: W L ⊂ S .

2. A challenger is randomly chosen, and then simultaneously both the incumbent and the challenger propose tax rates and policy provisions. Specifically, the challenger proposes his coalition, W c ⊂ S , a tax rate r c , and a provision of x c public and g C private goods. The incumbent proposes a tax rate r L , and policy provisions of x L public and g L private goods.

3. All selectors choose between the proposal of the challenger and the incumbent. The incumbent is removed and replaced by the challenger if and only if the challenger receives the support of at least W members of his nominated coalition ( W c ) and the incumbent retains less than W supporters from within her coalition ( W L ).

4. Each citizen allocates his or her resources between economically productive activities and leisure: l i∈ [0,1], where l i refers to individual i ’s leisure and (1 - l i ) refers to each individual’s level of economic activity, which we refer to as labor.

5. If the chosen leader’s policy provisions can be implemented, then they are. Otherwise a caretaker policy is implemented that gives everyone in the game a reservation payoff of v 0.By “can be implemented” we mean that revenues are sufficient to finance the proposed policies. Specifically, assuming the incumbent leader is retained, then saying that a proposed resource allocation can be implemented implies that

r L Σ i ∈ N (1 - l i ) - px L -| W L | g L = 0

Players receive payoffs, and the affinity preference ordering of the chosen leader is revealed.

In MPE, players condition their strategy on a state variable. In the current context, the state variable is the incumbent’s preference ordering over selectors—that is, the incumbent’s affinities. In addition to the standard equilibrium requirement that each player’s strategy must be utility maximizing given the strategy of the other players, the Markovian aspect of MPE insists that players condition their strategies only on the state variable—the incumbent’s ordering over selectors—and on no other aspect of the history of the game. In the MPE we characterize, this means leaders pick the selectors for whom they have the highest affinity when forming their coalitions. MPE also requires subgame perfection within a round.

There is an important difference between being in an incumbent’s winning coalition and being in a challenger’s first-period, transition coalition. The challenger does not know his affinity for individual supporters at the time he assembles his transition coalition. Of course this can be stated in a less stylized, more realistic way. The incumbent, who has had a greater opportunity to interact with and learn about the selectors than has the challenger, is more confident about her affinity toward selectors than the challenger since he is relatively unknown. From a modeling perspective, we sharpen this distinction by assuming a leader’s affinity ordering is unknown prior to coming to office but is fully revealed on coming to office. As we will see in chapter 7, relaxing this assumption so as to allow affinity to be learned gradually over time or to be known by both the challenger and the incumbent from the outset has important implications for the survival of leaders.