Bruce Mesquita - The Logic of Political Survival

Conclusion

We have defined the key players in our view of politics, how they are chosen, and what they do. Polities consist of leaders who try to stay in power. They always face challenges to that objective. Leaders stay in power by raising government revenue through taxation and then spending that revenue, dividing it between public-goods allocations that benefit everyone in the society and private rewards that go only to members of the winning coalition. To remain in office, leaders need to protect themselves against defections by members of their winning coalition. The coalition’s members are a subset of the selectorate, with members of the selectorate having the prospect of becoming members of a future winning coalition. Those in the current coalition are chosen, in part, based on their affinity. At the outset, when they back a would-be leader, they cannot be sure that once in power, the challenger will keep them on. The risk that they will be replaced increases as the selectorate gets larger and as the required coalition gets smaller. Those who are in the winning coalition beyond the transition period—that is, those in the coalition once the challenger is ensconced as the new incumbent—can be confident of remaining in the leader’s long-term coalition, since they were chosen because of their high affinity for the leader. Their primary benefit is the private rewards doled out to coalition members. Those who are neither the leader nor members of the winning coalition derive benefits only to the extent that the government provides public goods. They enjoy none of the private benefits that coalition members get.

Building on the relationship between coalition size and selectorate size, we develop a model that suggests a way to explain whether people face high taxation, receive many public benefits, live under the yoke of poverty, corruption, and rent seeking, or live in peace and prosperity.

3

A Model of the Selectorate Theory

In the previous chapter we introduced the core features of the selectorate theory. Here we put these components together in a rigorous mathematical manner to explain how selection institutions shape the political incentives. The mathematical structure of our theory forces us to be explicit about assumptions and logic. Although mathematical inference prevents us from making logical errors in our reasoning and allows others to see exactly where our deduction is wrong if we have erred, it does necessitate a substantial amount of mathematical notation. We have endeavored to minimize the mathematical presentation in the text by providing a formal appendix for the model at the end of the chapter. But we think it necessary to fully describe the model before explaining its logic in prose.

The selectorate model is an infinitely repeated game, meaning that leaders, selectors, and residents engage in the same form of political interaction over an indefinite series of rounds. We describe a single round here. The incumbent leader (denoted L ) is kept in power by a winning coalition of W members of the selectorate, where each member of the selectorate has equal weight in contributing to the winning coalition. We denote the members of the incumbent’s winning coalition W L . The incumbent always faces the prospect of being deposed by a challenger, denoted C .

A round begins with the incumbent picking a coalition, W L , of size W . 1A challenger is then randomly selected. Both the incumbent and the challenger simultaneously propose tax rates and the allocation of revenues between public and private goods. Additionally, the challenger selects a coalition, W C . Proposed expenditures can be less than tax revenue, but, by assumption, cannot exceed tax revenue. Later we investigate a conjecture about what happens if the budget constraint is relaxed and deficit spending is permitted. Any revenue raised through taxation that is not spent on providing public and private goods remains as funds available for the discretionary use of the leader. After the incumbent and challenger announce their tax proposal and their spending program, all members of the selectorate choose between the incumbent and the challenger. The incumbent is removed and replaced by the challenger if and only if the challenger receives the support of at least W members of his nominated coalition ( W C ) and the incumbent retains fewer than W supporters from within her coalition ( W L ). Each member of the society ( N ) allocates his or her personal resources (including time, energy, skills, money, and so on) between economically productive activities and leisure. Finally, the chosen leader’s policies are implemented. 2

We define r , subscripted with L or C as appropriate, to represent the tax rate proposed by the leader ( L ) or the challenger ( C ), while public goods are denoted x and private goods g , again with the appropriate subscript to indicate that the allocation was proposed by the leader or challenger. Leisure activity for individual i is said to equal l i with l i falling between 0 and 1, including 0 and 1 respectively. Productive activity equals (1 - l i ). For convenience, we refer to (1 - l i ) as labor, although it can be thought of as any kind of economic input.

Economic Activity, Policy Provision, and Payoffs

As mentioned, each citizen chooses to allocate resources between leisure and economic activity. While the nature of these resources could be viewed quite generally, for simplicity we do not differentiate types of economic activity or leisure, referring instead just to labor or leisure. If an individual chooses l i leisure, she contributes (1 - l i ) units of labor effort to economic activity. Given a tax rate of r , each individual retains (1 - r ) percent of the product of her economic activity. This means that an individual’s total retained level of personal economic product is equal to (1 - l i )(1 - r ). We sometimes denote this quantity y . Given each individual’s leisure-versus-labor decision, the overall level of economic activity in the society is equal to

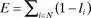
and so government revenue ( R ) equals rE .

When leaders or challengers propose the provision of public and private goods they take into account the cost of each type of good. The cost of public-goods provision is stipulated to equal p , while private goods have unit cost and all members of the coalition receive the same level of private goods. Consequently, the size of a leader’s coalition effectively acts as a price for private goods. That is, the cost to purchase a unit of private goods for her supporters is proportional to the number of people who must be rewarded: the size of the winning coalition.

The incumbent’s cost for providing x L public and g L private goods, given a coalition W L , is px L + | W L | g L , where the notation | W L | means the size of the set W L —that is, how many people are in the incumbent’s coalition. Rewards to the N residents in a society can come from four sources, although how much anyone receives from each source, if anything at all, varies with whether they are in the winning coalition or not. Everyone receives the benefits derived from the public goods provided by the government ( x ), while members of the winning coalition get their share of government-provided private goods ( g ) as well. Everyone enjoys the returns derived from the untaxed portion of their personal economic activity ( y ) and from leisure ( l ). Each individual’s utility function depends on these four components ( x , g , y , l ), and the utility function is posited to be an additively separable, smooth, twice-differentiable function, which is increasing and concave in each component. That is, the more of each component an individual gets, the greater that individual’s well-being. The more one gets, the less the additional increment to total utility, so that the function is increasing at a decreasing rate.