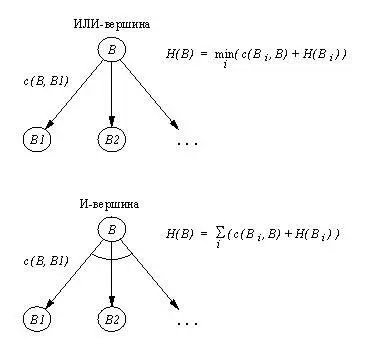
Рис. 13. 9. Получение оценки Н трудности задач И / ИЛИ-графа.
Обозначим через Н( В) оценку трудности вершины В . Для самой верхней вершины текущего дерева поиска H( В) просто совпадает с h( В) . С другой стороны, для оценки внутренней вершины дерева поиска нам не обязательно использовать непосредственно значение h , поскольку у нас есть некоторая дополнительная информация об этой вершине: мы знаем ее преемников. Следовательно, как показано на рис. 13.9, мы можем приближенно оценить трудность внутренней ИЛИ-вершины как
H( B) = min ( c( B, B i) + H( B i) )
i
где с( В, В) - стоимость дуги, ведущей из В в В i . Взятие минимума в этой формуле оправдано тем обстоятельством, что для того, чтобы решить задачу В , нам нужно решить только одну из ее задач-преемников. Трудность И-вершины В можно приближенно оценить так:
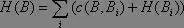
Будем называть H -оценку внутренней вершины "возвращенной" (backed-up) оценкой.
Более практичной с точки зрения использования в нашей программе поиска является другая величина F , которую можно определить в терминах H следующим образом. Пусть В1 - вершина-предшественник вершины В в дереве поиска, причем стоимость дуги, ведущей из В1 в В , равна с( В1, В) , тогда положим
F( B) = с( В1, В) + H( В)
Пусть В1 - родительская вершина вершины В , а В 1 , В 2 , ... - ее дочерние вершины, тогда, в соответствии с определениями F и H , имеем
F( B) = c( B1, B) + min F( B i), если В - ИЛИ-вершина
i
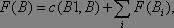 если В - И-вершина
если В - И-вершина
Хотя стартовая вершина А и не имеет предшественника, будем считать, что стоимость ведущей в нее (виртуальной) дуги равна 0. Если положить h равным 0 для всех вершин И / ИЛИ-дерева, то для любого найденного оптимального решающего дерева окажется, что его стоимость, т.е. сумма стоимостей его дуг, в точности равна F( A) .
На любой стадии поиска каждый преемник ИЛИ-вершины соответствует некоторому альтернативному решающему дереву-кандидату. Процесс поиска всегда принимает решение продолжать просмотр того дерева-кандидата, для которого F -оценка минимальна. Вернемся еще раз к рис. 13.4 и посмотрим, как будет вести себя процесс, поиска на примере И / ИЛИ-графа, изображенного на этом рисунке. В начале дерево поиска состоит всего из одной вершины - стартовой вершины а , далее дерево постепенно "растет" до тех пор, пока не будет найдено решающее дерево. На рис. 13.10, показан ряд "мгновенных снимков", сделанных в процессе роста дерева поиска. Для простоты мы предположим, что h = 0 для всех вершин. Числа, приписанные вершинам на рис. 13.10 - это их F -оценки (разумеется, по мере накопления информации в процессе поиска они изменяются). Ниже даются некоторые пояснительные замечания к рис. 13.10.
После распространения поиска из первоначального дерева (снимок А) получается дерево В. Вершина а - это ИЛИ-вершина, поэтому мы имеем два решающих дерева-кандидата: b и с . Поскольку F( b) = 1 < 3 = F( c) , для продолжения поиска выбирается альтернатива b . Насколько далеко может зайти процесс роста поддерева b ? Этот процесс может продолжаться до тех пор, пока не произойдет одно из двух событий:
(1) F -оценка вершины b станет больше, чем F -оценка ее конкурента с , или
(2) обнаружится, что найдено решающее дерево.
В связи с этим, начиная просмотр поддерева-кандидата b , мы устанавливаем верхнюю границу для F( b) : F( b) <= 3 = F( c) . Сначала порождаются преемники d и е вершины b (снимок С), после чего F -оценка b возрастает до 3. Так как это значение не превосходит верхнюю границу, рост дерева-кандидата с корнем в b продолжается. Вершина d оказывается целевой вершиной, а после распространения поиска из вершины е на один шаг получаем дерево, показанное на снимке D. В этот момент выясняется, что F( b) = 9 > 3 , и рост дерева b
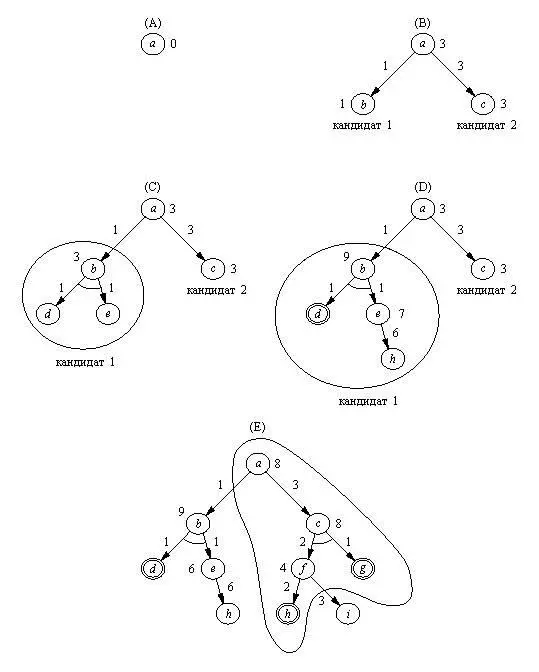
Рис. 13. 10. Трассировка процесса поиска с предпочтением в
Читать дальше


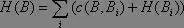
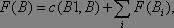 если В - И-вершина
если В - И-вершина



