Неизвестно - Prolog

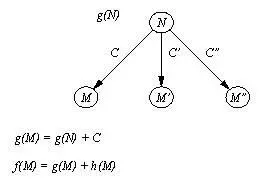
Рис. 12. 5. Связь между g- оценкой вершины В и f- и g- оценками

ее "детей" в пространстве состояний.

Алгоритм поиска пути называют допустимым , если он всегда отыскивает оптимальное решение (т.е. путь минимальной стоимости) при условии, что такой путь существует. Наша реализация алгоритма поиска, пользуясь механизмом возвратов, выдает все существующие решения, поэтому, в нашем случае, условием допустимости следует считать оптимальность первого из найденных решений. Обозначим через h*(n) стоимость оптимального пути из произвольной вершины n в целевую вершину. Верна следующая теорема о допустимости А*-алгоритма: А*-алгоритм, использующий эвристическую функцию h , является допустимым, если

h( n) <= h*( n)

для всех вершин n пространства состояний.

Этот результат имеет огромное практическое значение. Даже если нам не известно точное значение h* , нам достаточно найти какую-либо нижнюю грань h* и использовать ее в качестве h в А*-алгоритме - оптимальность решения будет гарантирована.

Существует тривиальная нижняя грань, а именно:

h( n) = 0, для всех вершин n пространства состояний.

И при таком значении h допустимость гарантирована. Однако такая оценка не имеет никакой эвристической силы и ничем не помогает поиску. А*-алгоритм при h= 0 ведет себя аналогично поиску в ширину. Он, действительно, превращается в поиск в ширину, если, кроме того, положить с(n, n' )= 1 для всех дуг (n, n') пространства состояний. Отсутствие эвристической силы оценки приводит к большой комбинаторной сложности алгоритма. Поэтому хотелось бы иметь такую оценку h , которая была бы нижней гранью h* (чтобы обеспечить допустимость) и, кроме того, была бы как можно ближе к h* (чтобы обеспечить эффективность). В идеальном случае, если бы нам была известна сама точная оценка h* , мы бы ее и использовали: А*-алгоритм, пользующийся h* , находит оптимальное решение сразу, без единого возврата.

Упражнение

12. 1. Определите отношения после, цельи h для задачи поиска маршрута рис. 12.2. Посмотрите, как наш алгоритм поиска с предпочтением будет вести себя при решении этой задачи.

Назад | Содержание | Вперёд

Назад | Содержание | Вперёд

12. 2. Поиск c предпочтением применительно к головоломке "игра в восемь"

Если мы хотим применить программу поиска с предпочтением, показанную на рис. 12.3, к какой-нибудь задаче, мы должны добавить к нашей программе отношения, отражающие специфику этой конкретной задачи. Эти отношения определяют саму задачу ("правила игры"), а также вносят в алгоритм эвристическую информацию о методе ее решения. Эвристическая информация задается в форме эвристической функции.

/* Процедуры, отражающие специфику головоломки

"игра в восемь".

Текущая ситуация представлена списком положений фишек;

первый элемент списка соответствует пустой клетке.

Пример:

3

2

1

1 2 3

8 4

7 6 5

1 2 3

Эта позиция представляется так:

[2/2, 1/3, 2/3, 3/3, 3/2, 3/1, 2/1, 1/1, 1/2]

"Пусто" можно перемещать в любую соседнюю клетку,

т.е. "Пусто" меняется местами со своим соседом.

*/

после( [Пусто | Спис], [Фшк | Спис1], 1) :-

% Стоимости всех дуг равны 1

перест( Пусто, Фшк, Спис, Спис1).

% Переставив Пусто и Фшк, получаем СПИС1

перест( П, Ф, [Ф | С], [П | С] ) :-

расст( П, Ф, 1).

перест( П, Ф, [Ф1 | С], [Ф1 | С1] ) :-

перест( П, Ф, С, С1).

расст( X/Y, X1/Y1, Р) :-

% Манхеттеновское расстояние между клетками

расст1( X, X1, Рх),

расст1( Y, Y1, Ру),

Р is Рх + Py.

расст1( А, В, Р) :-

Р is А-В, Р >= 0, ! ;

Р is B-A.

% Эвристическая оценка h равна сумме расстояний фишек

% от их "целевых" клеток плюс "степень упорядоченности",

% умноженная на 3

h( [ Пусто | Спис], H) :-

цель( [Пусто1 | Цспис] ),

сумрасст( Спис, ЦСпис, Р),

упоряд( Спис, Уп),

Н is Р + 3*Уп.

сумрасст( [ ], [ ], 0).

сумрасст( [Ф | С], [Ф1 | С1], Р) :-

расст( Ф, Ф1, Р1),

сумрасст( С, Cl, P2),

Р is P1 + Р2.

упоряд( [Первый | С], Уп) :-

упоряд( [Первый | С], Первый, Уп).

упоряд( [Ф1, Ф2 | С], Первый, Уп) :-

очки( Ф1, Ф2, Уп1),