Неизвестно - Prolog

Дер Текущее (под)дерево поиска.

Предел Предельное значение f -оценки, при котором допускается расширение.

Дер1 Дерево Дер, расширенное в пределах ограничения Предел;

f -оценка дерева Дер1больше, чем Предел( если только при расширении не была обнаружена целевая вершина).

ЕстьРеш Индикатор, принимающий значения "да", "нет" и "никогда".

Решение Решающий путь, ведущий из стартовой вершины через дерево Дер1

к целевой вершине и имеющий стоимость, не превосходящую ограничение Предел(если такая целевая вершина была обнаружена).

Переменные Путь, Дер, и Предел- это "входные" параметры процедуры расширитьв том смысле, что при каждом обращении к расширитьони всегда конкретизированы. Процедура расширитьпорождает результаты трех видов. Какой вид результата получен, можно определить по значению индикатора ЕстьРешследующим образом:

(1) ЕстьРеш = да.

Решение= решающий путь, найденный при расширении дерева Дерс учетом ограничения Предел.

Дер1= неконкретизировано.

(2) ЕстьРеш = нет

Дер1= дерево Дер, расширенное до тех пор, пока его f -оценка не превзойдет Предел(см. рис. 12.4).

Решение= неконкретизировано.

(3) ЕстьРеш = никогда.

Дер1и Решение= неконкретизированы.

В последнем случае Дерявляется "тупиковой" альтернативой, и соответствующий процесс никогда не будет реактивирован для продолжения просмотра этого дерева. Случай этот возникает тогда, когда f -оценка дерева Дерне превосходит ограничения Предел, однако дерево не может "расти" потому, что ни один его лист не имеет преемников, или же любой преемник порождает цикл.

Некоторые предложения процедуры расширитьтребуют пояснений. Предложение, относящееся к наиболее сложному случаю, когда Деримеет поддеревья, т.е.

Дер = д( В, F/G, [Д | ДД ] )

означает следующее. Во-первых, расширению подвергается наиболее перспективное дерево Д. В качестве ограничения этому дереву выдается не Предел, а не-

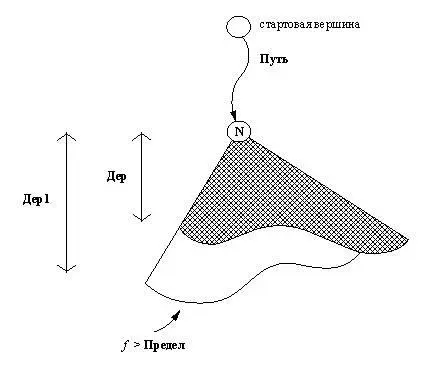
Рис. 12. 4. Отношение расширить: расширение дерева Дердо тех

пор, пока f -оценка не превзойдет Предел, приводит к дереву Дер1.

которое, возможно, меньшее значение Предел1, зависящее от f -оценок других конкурирующих поддеревьев ДД. Тем самым гарантируется, что "растущее" дерево - это всегда наиболее перспективное дерево, а переключение активности между поддеревьями происходит в соответствии с их f -оценками. После того, как самый перспективный кандидат расширен, вспомогательная процедура продолжитьрешает, что делать дальше, а это зависит от типа результата, полученного после расширения. Если найдено решение, то оно и выдается, в противном случае процесс расширения деревьев продолжается.

Предложение, относящееся к случаю

Дер = л( В, F/G)

порождает всех преемников вершины Ввместе со стоимостями дуг, ведущих в них из В. Процедура преемсписформирует список поддеревьев, соответствующих вершинам-преемникам, а также вычисляет их g- и f- оценки, как показано на рис. 12.5. Затем полученное таким образом дерево подвергается расширению с учетом ограничения Предел. Если преемников нет, то переменной ЕстьРешпридается значение "никогда" и в результате лист Впокидается навсегда.

Другие отношения:

после( В, В1, С) В1 - преемник вершины В; С- стоимость дуги, ведущей из В в В1.

h( В, Н) Н - эвристическая оценка стоимости оптимального пути

из вершины В в целевую вершину.

макс_f( Fмакс) Fмакс - некоторое значение, задаваемое пользователем,

про которое известно, что оно больше любой возможной f -оценки.

В следующих разделах мы покажем на примерах, как можно применить нашу программу поиска с предпочтением к конкретным задачам. А сейчас сделаем несколько заключительных замечаний общего характера относительно этой программы. Мы реализовали один из вариантов эвристического алгоритма, известного в литературе как А*-алгоритм (ссылки на литературу см. в конце главы). А*-алгоритм привлек внимание многих исследователей. Здесь мы приведем один важный результат, полученный в результате математического анализа А*-алгоритма: