Неизвестно - Prolog

11. 2. Стратегия поиска в глубину

Существует много различных подходов к проблеме поиска решающего пути для задач, сформулированных в терминах пространства состояний. Основные две стратегии поиска - это поиск в глубину и поиск в ширину . В настоящем разделе мы реализуем первую из них.

Мы начнем разработку алгоритма и его вариантов со следующей простой идеи:

Для того, чтобы найти решающий путь Решиз заданной вершины Вв некоторую целевую вершину, необходимо:

если В- это целевая вершина, то положить Реш = [В], или

если для исходной вершины Всуществует вершина-преемник В1, такая, что можно провести путь Реш1из В1в целевую вершину, то положить Реш = [В | Peш1].

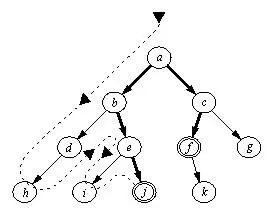
Рис. 11. 4. Пример простого пространства состояний: а - стартовая

вершина, f и j - целевые вершины. Порядок, в которой происходит

проход по вершинам пространства состояний при поиске в глубину:

а , b , d , h , e , i , j . Найдено решение [a, b, e, j]. После возврата

обнаружено другое решение: [а, с, f].

На Пролог это правило транслируется так:

решить( В, [В] ) :-

цель( В).

решить( В, [В | Реш1] ) :-

после( В, В1 ),

решить( В1, Реш1).

Эта программа и есть реализация поиска в глубину. Мы говорим "в глубину", имея в виду тот порядок, в котором рассматриваются альтернативы в пространстве состояний. Всегда, когда алгоритму поиска в глубину надлежит выбрать из нескольких вершин ту, в которую следует перейти для продолжения поиска, он предпочитает самую "глубокую" из них. Самая глубокая вершина - это вершина, расположенная дальше других от стартовой вершины. На рис. 11.4 мы видим на примере, в каком порядке алгоритм проходит по вершинам. Этот порядок в точности соответствует результату трассировки процесса вычислений в пролог-системе при ответе на вопрос

?- решить( а, Реш).

Поиск в глубину наиболее адекватен рекурсивному стилю программирования, принятому в Прологе. Причина этого состоит в том, что, обрабатывая цели, пролог-система сама просматривает альтернативы именно в глубину.

Поиск в глубину прост, его легко программировать и он в некоторых случаях хорошо работает. Программа для решения задачи о восьми ферзях (см. гл. 4) фактически была примером поиска в глубину. Для того, чтобы можно было применить к этой задаче описанную выше процедуру решить, необходимо сформулировать задачу в терминах пространства состояний. Это можно сделать так:

вершины пространства состояний - позиции, в которых поставлено 0 или более ферзей на нескольких последовательно расположенных горизонтальных линиях доски;

вершина-преемник данной вершины может быть получена из нее после того, как в соответствующей позиции на следующую горизонтальную линию доски будет поставлен еще один ферзь, причем таким образом, чтобы ни один из уже поставленных ферзей не оказался под боем;

стартовая вершина - пустая доска (представляется пустым списком);

целевая вершина - любая позиция с восемью ферзями (правило получения вершины-преемника гарантирует, что ферзи не бьют друг друга).

Позицию на доске будем представлять как список Y-координат поставленных ферзей. Получаем программу:

после( Ферзи, [Ферзь | Ферзи] ) :-

принадлежит( Ферзь, [1, 2, 3, 4, 5, 6, 7, 8] ),

% Поместить ферзя на любую вертикальную линию

небьет( Ферзь, Ферзи).

цель( [ _, _, _, _, _, _, _, _ ] )

% Позиция с восемью ферзями

Отношение небьетозначает, что Ферзьне может поразить ни одного ферзя из списка Ферзи. Эту процедуру можно легко запрограммировать так же, как это сделано в гл. 4. Ответ на вопрос

?- решить( [ ], Решение)

будет выглядеть как список позиций с постепенно увеличивающимся количеством поставленных ферзей. Список завершается "безопасной" конфигурацией из восьми ферзей. Механизм возвратов позволит получить и другие решения задачи.

Поиск в глубину часто работает хорошо, как в рассмотренном примере, однако наша простая процедура решитьможет попасть в затруднительное положение, причем многими способами. Случится ли это или нет - зависит от структуры пространства состояний. Для того, чтобы затруднить работу процедуры решить в примере рис. 11.4, достаточно внести в задачу совсем небольшое изменение: добавить дугу, ведущую из h в d , чтобы получился цикл (рис. 11.5). В этом случае поиск будет выглядеть так: начиная с вершины а , спускаемся вплоть до h , придерживаясь самой левой ветви графа. На этот раз, в отличие от рис. 11.4, у вершины h будет преемник d . Поэтому произойдет не возврат из h , а переход к d . Затем мы найдем преемника вершины d , т.е. вершину h , и т.д., в результате программа зациклится между h и d .