Неизвестно - Prolog

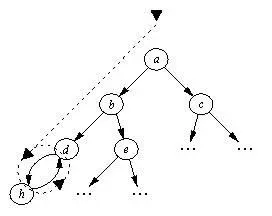
Рис. 11. 5. Начинаясь в а , поиск вглубину заканчивается

бесконечным циклом между d и h : a , b , d , h , d , h , d ... .

Очевидное усовершенствование нашей программы поиска в глубину - добавление к ней механизма обнаружения циклов. Ни одну из вершин, уже содержащихся в пути, построенном из стартовой вершины в текущую вершину, не следует вторично рассматривать в качестве возможной альтернативы продолжения поиска. Это правило можно сформулировать в виде отношения

вглубину( Путь, Верш, Решение)

Как видно из рис. 11.6, Верш- это состояние, из которого необходимо найти путь до цели; Путь- путь (список вершин) между стартовой вершиной и Верш; Решение- Путь, продолженный до целевой вершины.

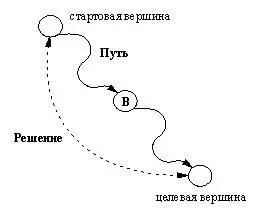
Рис. 11. 6. Отношение вглубину( Путь, В, Решение).

Для облегчения программирования вершины в списках, представляющих пути, будут расставляться в обратном порядке. Аргумент Путьнужен для того,

(1) чтобы не рассматривать тех преемников вершины Верш, которые уже встречались раньше (обнаружение циклов);

(2) чтобы облегчить построение решающего пути Решение. Соответствующая программа поиска в глубину показана на рис. 11.7.

решить( Верш, Решение) :-

вглубину( [ ], Верш, Решение).

вглубину( Путь, Верш, [Верш | Путь] ) :-

цель( Верш).

вглубину( Путь, Верш, Реш) :-

после( Верш, Верш1),

not принадлежит( Верш1, Путь), % Цикл ?

вглубину( [Верш | Путь], Верш1, Реш).

Рис. 11. 7. Программа поиска в глубину без зацикливания.

Теперь наметим один вариант этой программы. Аргументы Путьи Вершпроцедуры вглубинуможно объединить в один список [Верш | Путь]. Тогда, вместо вершины-кандидата Верш, претендующей на то, что она находится на пути, ведущем к цели, мы будем иметь путь -кандидат П = [Верш | Путь], который претендует на то, что его можно продолжить вплоть до целевой вершины. Программирование соответствующего предиката

вглубину( П, Решение)

оставим читателю в качестве упражнения.

Наша процедура поиска в глубину, снабженная механизмом обнаружения циклов, будет успешно находить решающие пути в пространствах состояний, подобных показанному на рис. 11.5. Существуют, однако, такие пространства состоянии, в которых наша процедура не дойдет до цели. Дело в том, что многие пространства состояний бесконечны. В таком пространстве алгоритм поиска в глубину может "потерять" цель, двигаясь вдоль бесконечной ветви графа. Программа будет бесконечно долго обследовать эту бесконечную область пространства, так и не приблизившись к цели. Пространство состояний задачи о восьми ферзях, определенное так, как это сделано в настоящем разделе, на первый взгляд содержит ловушку именно такого рода. Но оказывается, что оно все-таки конечно, поскольку Y-координаты выбираются из ограниченного множества, и поэтому на доску можно поставить "безопасным образом" не более восьми ферзей.

вглубину2( Верш, [Верш], _ ) :-

цель( Верш).

вглубину2( Верш, [Верш | Реш], МаксГлуб) :-

МаксГлуб > 0,

после( Верш, Верш1),

Maкс1 is МаксГлуб - 1,

вглубину2( Верш1, Реш, Maкс1).

Рис. 11. 8. Программа поиска в глубину с ограничением по глубине.

Для того, чтобы предотвратить бесцельное блуждание по бесконечным ветвям, мы можем добавить

в базовую процедуру поиска в глубину еще одно усовершенствование, а именно, ввести

ограничение на глубину поиска

. Процедура поиска в глубину будет тогда иметь следующие аргументы:

вглубину2( Верш, Решение, МаксГлуб)

Не разрешается вести поиск на глубине большей, чем МаксГлуб. Программная реализация этого ограничения сводится к уменьшению на единицу величины предела глубины при каждом рекурсивном обращений к вглубину2и к проверке, что этот предел не стал отрицательным. В результате получаем программу, показанную на рис. 11.8.

Упражнения

11. 1. Напишите процедуру поиска в глубину (с обнаружением циклов)