Feynmann - Feynmann 9

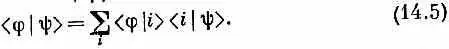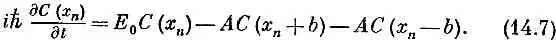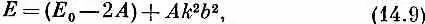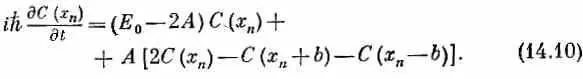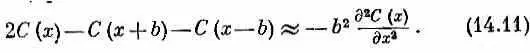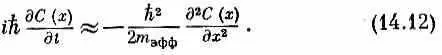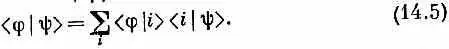
Суммирование, конечно, проводится по всей совокупности ба­зисных состояний | i > .

В гл. 11, когда мы рассчитывали, что бывает с электроном, помещенным в линейную цепочку атомов, вы выбрали совокуп­ность базисных состояний, в которых электрон был расположен близ того или иного из атомов цепочки. Базисное состояние | n > представляло электрон, локализованный (расположенный) возле атома номер п. (Конечно, неважно, обозначать ли наши базисные состояния | n > или | i >.) Чуть позже мы нашли, что базисные состояния удобнее метить координатой атома, а не номером атома в цепочке. Состояние | х n > — это просто другой способ записи состояния | n >. Тогда, следуя общему правилу, любое состояние |y> можно описать заданием того, что электрон в состоянии |y> находится также в одном из состояний | х n > . Для удобства мы решили обозначать эти амплитуды символом

C n = < x n |y>. (14.6)

Поскольку базисные состояния связаны с местоположением электрона на линии, то амплитуду С n можно рассматривать как функцию координаты х и писать ее в виде С ( х n ) . Амплитуды С ( х n ) будут в общем случае меняться во времени и поэтому суть также функции от t , но мы не будем отмечать эту зависи­мость явно.

Кроме того, в гл. 11 мы предположили, что амплитуды С(х n ) обязаны меняться во времени так, как положено по гамильтонову уравнению (11.3). В нашем новом обозначении это уравне­ние имеет вид

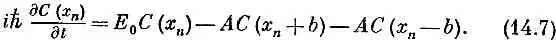
Два последних слагаемых в правой части представляют такой процесс, когда электрон, находившийся возле атома ( n +1) или возле атома ( n - 1), окажется возле атома ( n ).

Мы нашли, что (14.7) имеет решения, отвечающие состоя­ниям определенной энергии. Мы записывали их в виде

У состояний с низкой энергией длины волн велики ( k мало) и энергия связана с k формулой

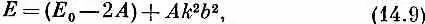
или, если выбрать нуль энергии так, чтобы было (Е 0 - 2 А) = 0, то энергия дается формулой (14.1).

Посмотрим, что бы произошло, если бы мы позволили рас­стоянию b между атомами решетки стремиться к нулю, сохра­няя волновое число постоянным. Если бы больше ничего не случилось, то последнее слагаемое в (14.9) обратилось бы просто в нуль, и никакой физики бы не осталось. Но предположим, что А и b вместе изменяются так, что при стремлении b к нулю произведение Ab 2 поддерживается постоянным: с помощью (14.2) мы запишем А b 2 в виде постоянной h 2 /2m эфф . При этом (14.9) не изменится, но что произойдет с дифференциальным уравнением (14.7)?

Перепишем сперва (14.7) так:

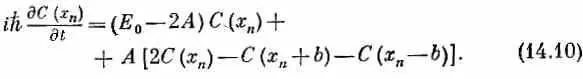
При нашем выборе Е 0 первое слагаемое выпадет. Далее, пред­ставим себе непрерывную функцию С ( х ) , которая плавно про­ходит через значения С ( х n ) в точках х n . Когда расстояние b стремится к нулю, точки х n сближаются все теснее и теснее и [если С ( х ) меняется достаточно плавно] величина в скобках попросту пропорциональна второй производной С ( х ) . Можно написать (в чем легко убедиться, разложив в ряд Тэйлора каждый член) равенство

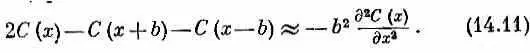
Тогда в пределе, когда b стремится к нулю, а b 2 A поддерживает­ся равным h2 /2 m эфф , уравнение (14.7) переходит в

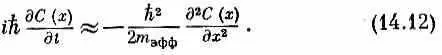
Перед нами уравнение, утверждающее, что скорость изменения С ( х ) — амплитуды того, что электрон будет обнаружен в х— зависит от амплитуды того, что электрон будет обнаружен в близлежащих точках так, что эта скорость пропорциональна второй производной амплитуды по координате.