Feynmann - Feynmann 8a

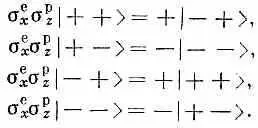
Если перебрать все допустимые операторы, каждый по разу, то всего может быть 16 возможностей. Да, шестнадцать, если включить еще «единичный оператор» 1. Во-первых, есть тройка s е х , s е y , s е z , затем тройка s p x, s p y, s p z, итого шесть. Кроме того, имеет­ся девять произведений вида s е х s p y, итого 15. И еще единичный оператор, оставляющий все состояния нетронутыми. Вот и все шестнадцать!

Заметьте теперь, что для системы с четырьмя состояниями матрица Гамильтона должна представлять собой матрицу коэф­фициентов 4x4, в ней будет 16 чисел. Легко показать, что всякая матрица 4X4, и в частности матрица Гамильтона, может быть записана в виде линейной комбинации шестнадцати двой­ных спиновых матриц, соответствующих системе операторов, которые мы только что составили. Поэтому для взаимодействия между протоном и электроном, в которое входят только их спины, мы можем ожидать, что оператор Гамильтона может быть записан в виде линейной комбинации тех же 16 операторов. Вопрос только в том, как.

Но, во-первых, мы знаем, что взаимодействие не зависит от нашего выбора осей для системы координат. Если нет внеш­него возмущения — чего-то вроде магнитного поля, выделяю­щего какое-то направление в пространстве,— то гамильтониан не может зависеть от нашего выбора направлений осей х, у и z . Это означает, что в гамильтониане не может быть таких членов, как s e xсам по себе. Это выглядело бы нелепо, потому что кто-нибудь в другой системе координат пришел бы к другим резуль­татам.

Единственно возможны только член с единичной матрицей, скажем постоянная а (умноженная на 1^), и некоторая комбина­ция сигм, которая не зависит от координат, некоторая «инва­риантная» комбинация. Единственная скалярная инвариантная комбинация из двух векторов — это их скалярное произведе­ние, имеющее для наших сигм вид

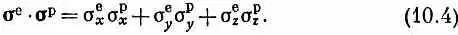
Этот оператор инвариантен по отношению к любому повороту системы координат. Итак, единственная возможность для га­мильтониана с подходящей симметрией в пространстве — это постоянная, умноженная на единичную матрицу, плюс постоян­ная, умноженная на это скалярное произведение, т. е.

Это и есть наш гамильтониан. Это единственное, чему, исходя из симметрии в пространстве, он может равняться, пока нет внешнего поля. Постоянный член нам многого не сообщит; он просто зависит от уровня, который мы выбрали для отсчета энергий. С равным успехом можно было принять Е 0=0. А второй член поведает нам обо всем, что нужно для того, чтобы найти расщепление уровней в водороде.

Если угодно, можно размышлять о гамильтониане иначе. Если поблизости друг от друга находятся два магнита с магнит­ными моментами m еи m р, то их взаимная энергия зависит, кроме всего прочего, и от m е · m р. А мы, как вы помните, выяснили, что та вещь, которую мы в классической физике называли m е , в квантовой механике выступает под именем m es e. Подобным же образом, то, что в классической физике выглядит как m p, в кван­товой механике обычно оказывается равным m рs р(где m р— маг­нитный момент протона, который почти в 1000 раз меньше m еи имеет обратный знак). Значит, (10.5) утверждает, что энергия взаимодействия подобна взаимодействию двух магнитов, но не до конца, потому что взаимодействие двух магнитов зависит от расстояния между ними. Но (10.5) может считаться (и на самом деле является) своего рода средним взаимодействием. Электрон как-то движется внутри атома, и .наш гамильтониан дает лишь среднюю энергию взаимодействия. В общем все это говорит о том, что для предписанного расположения электрона и протона в пространстве существует энергия, пропорциональ­ная косинусу угла между двумя магнитными моментами (выра­жаясь классически). Такая классическая качественная картина может помочь вам понять, откуда все получается, но единственное что важно при этом то, что (10.5) — это правильная квантовомеханическая формула.

Порядок величины классического взаимодействия между двумя магнитами должен был бы даваться произведением двух магнитных моментов, деленным на куб расстояния между ними. Расстояние между электроном и протоном в атоме водорода, грубо говоря, равно половине атомного радиуса, т. е. 0,5 А. Поэтому можно примерно прикинуть, что постоянная А должна быть равна произведению магнитных моментов m еи m p, делен­ному на куб половины ангстрема. Такая пристрелка приводит к числам, попадающим как раз в нужный район. Но оказывается, что А можно подсчитать и аккуратней, стоит только разобраться в полной теории атома водорода, что нам пока не по силам. На самом деле А было подсчитано с точностью до 30 миллион­ных. Как видите, в отличие от постоянной переброса А молекулы аммиака, которую по теории невозможно хорошо подсчитать, наша постоянная А для водорода может быть рассчитана из более детальной теории. Но ничего не поделаешь, нам для наших теперешних целей придется считать А числом, которое может быть определено из опыта, и анализировать физику дела.