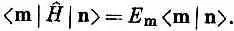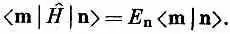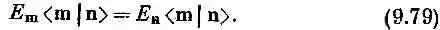Feynmann - Feynmann 8a

Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть | n> и | m> — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния | m> и умножив его на | n>, получим

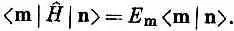
Но если (9.71) умножить на < m|, то будет

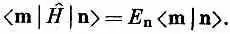
Раз левые части этих уравнений равны, то равны и правые:

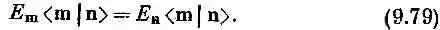
Если Е m =Е n , то это равенство ни о чем не говорит. Но если энергии двух состояний | m> и | n> различны (Е m № Е n ), то урав­нение (9.79) говорит, что < m| n> должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Е n и Е m отличаются друг от друга.

* Такую интерференцию действительно наблюдали. Коэффициент a оказался равным — 0,96 b . Отсюда можно было вычислить и разность масс К 1 - и K 2 -мезонов. Она оказалась равной около —0,35 · 10 -5 эв. Это наимень­шая разность масс двух частиц, известных физикам.— Прим. ред.

* Мы здесь упрощаем. Система 2 p может иметь множество состоя­ний, отвечающих различным импульсам p -мезонов, и в правой части >того равенства следовало бы поставить сумму по всем базисным состоя­ниям p -мезонов. Но полный вывод все равно приводит к тем же резуль­татам.

* Типичное время для сильного взаимодействия ближе к 10 -23 сек.

* Если, конечно, он не создает еще двух К + или других частиц с общей странностью +2. Можно считать, что здесь речь идет о реакциях, в которых не хватает энергии для возникновения этих добавочных стран­ных частиц.

** Свободная L -частица медленно распадается путем слабого взаимо­действия (так что странность не обязана при этом сохраняться). Про­дуктами распада могут быть либо р и p - , либо n и p 0 . Время жизни 2,2 · 10 -1 0 сек.

* Читайте: «. K -нуль с чертой».

** Среди новых частиц есть барион W - со странностью -3 .—Прим. ред.

* Это похоже на то, что мы обнаружили (в гл. 4) для частиц со спи­ном 1 / 2 . когда поворачивали систему координат вокруг оси z ; тогда мы получили фазовые множители exp (± i j /2). В действительности это в точ­ности то же самое, что мы писали в гл. 3, § 7, для состояний | + > и | - > частицы со спином 1, и это не случайно. Фотон— это частица со спи­ном 1, у которой, однако, нет «нуль»-состояния.

** Мы сознаем, что материал этого параграфа длиннее и труднее, чем это положено на нашем уровне знаний. Лучше пропустите его и пере­ходите прямо к § 6. Но если у вас есть самолюбие и время, попозже вер­нитесь к нему опять. Это великолепнейший пример (взятый к тому же из последних работ по физике высоких энергий) того, что можно сотворить с помощью нашей формулировки квантовой механики двухуровневых систем. (Для русского издания параграф переделан проф. Сэндсом. — Прим. ред.)

* Параграф 5 при первом чтении книги можно пропустить. Он сложнее, чем положено в таких курах.

Глава 10

СВЕРХТОНКОЕ РАСЩЕПЛЕНИЕ В ВОДОРОДЕ

§ 1. Базисные состо­яния для системы двух частиц со спином 1/2