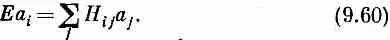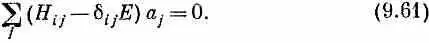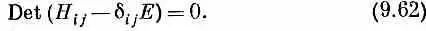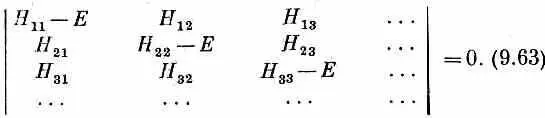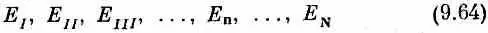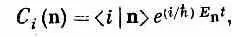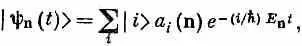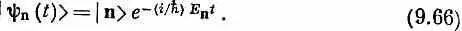Feynmann - Feynmann 8a

Мы нашли общее решение для всех С в системе с двумя со­стояниями, когда энергетическая матрица постоянна (не зави­сит от t ). Точно так же нетрудно решить и уравнение (9.58) для системы с N состояниями, когда Н не зависит от времени. Опять мы начинаем с того, что ищем возможное решение, в кото­ром у всех амплитуд зависимость от времени одинакова. Мы про­буем

Если все эти C i подставить в (9.58), то производные dC i ( t ) / dt превращаются просто в (- i / h ) EC i . Сокращая повсюду на общую экспоненту, получаем

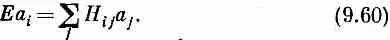
Эта система N линейных алгебраических уравнений для N неизвестных a 1 а 2, . . ., а n ; решение у нее бывает только тогда, когда вам сильно повезет, когда определитель из коэффициентов при всех а равен нулю. Но не нужно чересчур умничать: можете просто начать их решать любым способом, и вы сразу увидите, что решить их удается лишь при некоторых значениях E . (Вспомните, что единственная величина, которая в этих уравне­ниях подлежит подгонке, это Е.)

Если, впрочем, вы хотите, чтобы все было по форме, пере­пишите (9.60) так:

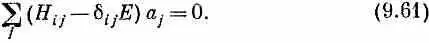
Затем примените правило (если оно вам знакомо), что эти урав­нения будут иметь решения лишь для тех значений Е, для кото­рых

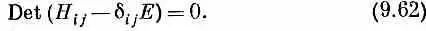
Каждый член в детерминанте — это просто H ij и только из диагональных отнято Е. Иначе говоря, (9.62) означает просто

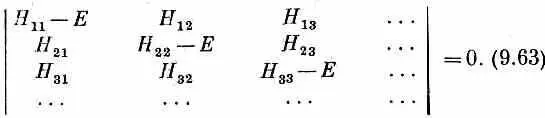
Это, конечно, всего-навсего особый способ записывать алгебраи­ческие уравнения для Е, складывая вереницы членов, пере­множаемых в определенном порядке. Эти произведения дадут все степени Е вплоть до E N .

Значит, у нас есть многочлен N - й степени, который равняется нулю. У него, вообще говоря, есть N корней. (Нужно помнить, однако, что некоторые из них могут быть кратными корнями; это значит, что два или более корней могут быть равны друг другу.) Обозначим эти N корней так:

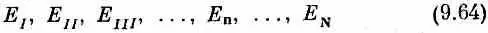
(пусть nобозначает n -е порядковое числительное, так что n принимает значения I , II , . . ., N). Некоторые из этих энергий могут быть между собой равны, скажем Е II = Е III , но мы решили все же обозначать их разными именами.

Уравнения (9.60) или (9.61) имеют по одному решению для каждого значения Е [из (9.64)]. Если вы подставите любое из Е, скажем E n , в (9.60) и найдете все а i , то получится ряд чисел а i , относящихся к энергии E n . Этот ряд мы обозначим а i ( n).

Если подставить эти а i ( n) в (9.59), то получатся амплитуды С i ( n) того, что состояния с определенной энергией находятся в базисном состоянии | i >. Пусть | n> обозначает вектор состоя­ния для состояния с определенной энергией при t = 0 . Тогда можно написать

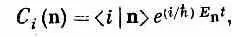
где

Полное состояние с определенной энергией |y n( t )> можно тогда записать так:

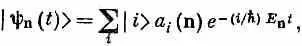
или

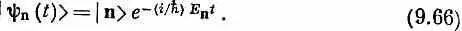
Векторы состояний | n> описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от вре­мени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.