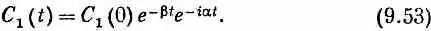
Вероятность обнаружить в момент t частицу К 1 равна квадрату модуля этой амплитуды, т. е. e -2 b t . А из (9.52) следует, что вероятность обнаружить в любой момент состояние K 2 равна нулю. Это значит, что если вы создаете К -мезон в состоянии | К 1>, то вероятность найти его в том же состоянии со временем экспоненциально падает, но вы никогда не увидите его в состоянии | К 2> . Куда же он девается? Он распадается на два p-мезона со средним временем жизни t= 1/ 2b, экспериментально равным 10 -1 0 сек. Мы предусмотрели это, говоря, что А комплексное.
С другой стороны, (9.52) утверждают, что если создать . K -мезон целиком в состоянии К 2 , он останется в нем навсегда. На самом-то деле это не так. На опыте замечено, что он распадается на три p-мезона, но в 600 раз медленнее, чем при описанном нами двухпионном распаде. Значит, имеются какие-то другие малые члены, которыми мы в нашем приближении пренебрегли. Но до тех пор, пока мы рассматриваем только двухпионные распады, К 2 остается «навсегда».
Рассказ о Гелл-Манне и Пайсе близится к концу. Дальше они посмотрели, что будет, когда K -мезон образуется вместе с L 0 -частицей в сильном взаимодействии. Раз его странность должна быть +1, он обязан возникать в состоянии К 0 , Значит, при t =0 он не является ни К 1 , ни К 2 , а их смесью. Начальные условия таковы:

Но это означает [из (9.50)], что
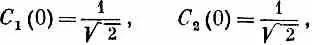
а из (9.52) следует, что
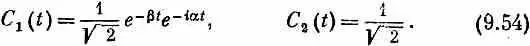
Теперь вспомним, что K 1и К 2 суть линейные комбинации К 0 и К°. В (9.54) амплитуды были выбраны так, что при t =0 части,
из которых состоит 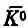 , взаимно уничтожаются за счет интерференции, оставляя только состояние К 0 . Но состояние | К 1> со временем меняется, а состояние | К 2> — нет . После t = 0 интерференция С 1 и С 2приведет к конечным амплитудам и для К 0 , и для
, взаимно уничтожаются за счет интерференции, оставляя только состояние К 0 . Но состояние | К 1> со временем меняется, а состояние | К 2> — нет . После t = 0 интерференция С 1 и С 2приведет к конечным амплитудам и для К 0 , и для 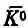 .
.
Что же все это значит? Возвратимся назад и подумаем об опыте, показанном на фиг. 9.5. Там p --мезон образовал L 0-частицу и K 0-мезон, который летит без оглядки сквозь водород камеры. Когда он движется, существует ничтожный, но постоянный шанс, что он столкнется с ядром водорода. Раньше мы думали, что сохранение странности предохранит K-мезон от образования L 0-частицы в таком взаимодействии. Теперь, однако, мы понимаем, что это не так. Потому что, хотя наш К-мезон вначале является К 0-мезоном, неспособным к рождению L°-частицы, он не остается им навечно. Через мгновение появляется некоторая амплитуда того, что он перейдет в состояние 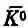 . Значит, следует ожидать, что иногда мы увидим L 0-частицу, образованную вдоль следа K -мезона. Вероятность такого происшествия дается амплитудой С - , которую можно [решая (9.50)] связать с С 1 и С 2. Связь эта такова:
. Значит, следует ожидать, что иногда мы увидим L 0-частицу, образованную вдоль следа K -мезона. Вероятность такого происшествия дается амплитудой С - , которую можно [решая (9.50)] связать с С 1 и С 2. Связь эта такова:
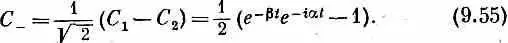
И когда K -частица движется, вероятность того, что она будет «действовать как» 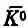 , равна | С - | 2 , т. е.
, равна | С - | 2 , т. е.
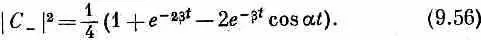
Сложный и поразительный результат!
Это и есть замечательное предсказание Гелл-Манна и Пайса: когда возникает K 0-мезон, то шанс, что он превратится в 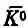 - мезон, продемонстрировав это возможностью создания L 0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутренних механизмов K -частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально наблюдаемой скорости распада на два p-мезона (2b=1,1·10 10 сек -1), но про a они ничего не смогли сказать.
- мезон, продемонстрировав это возможностью создания L 0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутренних механизмов K -частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально наблюдаемой скорости распада на два p-мезона (2b=1,1·10 10 сек -1), но про a они ничего не смогли сказать.
Читать дальше

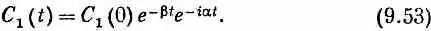

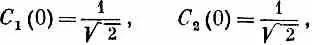
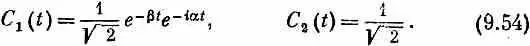
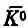 , взаимно уничтожаются за счет интерференции, оставляя только состояние К 0 . Но состояние | К 1> со временем меняется, а состояние | К 2> — нет . После t = 0 интерференция С 1 и С 2приведет к конечным амплитудам и для К 0 , и для
, взаимно уничтожаются за счет интерференции, оставляя только состояние К 0 . Но состояние | К 1> со временем меняется, а состояние | К 2> — нет . После t = 0 интерференция С 1 и С 2приведет к конечным амплитудам и для К 0 , и для 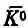 .
.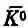 . Значит, следует ожидать, что иногда мы увидим L 0-частицу, образованную вдоль следа K -мезона. Вероятность такого происшествия дается амплитудой С - , которую можно [решая (9.50)] связать с С 1 и С 2. Связь эта такова:
. Значит, следует ожидать, что иногда мы увидим L 0-частицу, образованную вдоль следа K -мезона. Вероятность такого происшествия дается амплитудой С - , которую можно [решая (9.50)] связать с С 1 и С 2. Связь эта такова: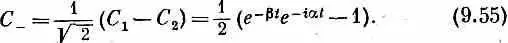
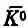 , равна | С - | 2 , т. е.
, равна | С - | 2 , т. е.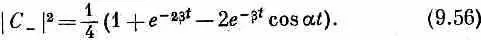
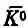 - мезон, продемонстрировав это возможностью создания L 0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутренних механизмов K -частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально наблюдаемой скорости распада на два p-мезона (2b=1,1·10 10 сек -1), но про a они ничего не смогли сказать.
- мезон, продемонстрировав это возможностью создания L 0-частицы, меняется со временем по закону (9.56). Это предсказание последовало только из чистейших логических рассуждений и из основных принципов квантовой механики без знания внутренних механизмов K -частицы. И поскольку никто не знает ничего об этом внутреннем механизме, то дальше этого Гелл-Манн и Пайс не смогли продвинуться. Им не удалось дать теоретических значений a и b. И никто до сегодняшнего дня не смог это сделать. Им было по силам оценить значение b из экспериментально наблюдаемой скорости распада на два p-мезона (2b=1,1·10 10 сек -1), но про a они ничего не смогли сказать.










